thegirl
- 40
- 1
In the case of two fields interfering with each other when calculating the total electric field, cos (phi1-phi2 + kx) = cos( kx) where kx is the path difference between the two fields.
How does cos (phi1-phi2 +kx)=cos(kx) Isit just algebra?
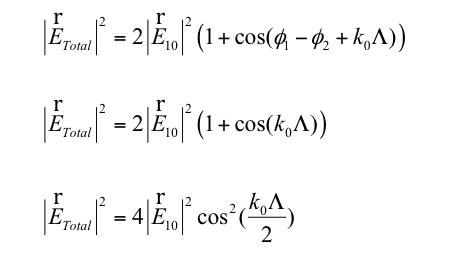
How does cos (phi1-phi2 +kx)=cos(kx) Isit just algebra?