Why Does Crank-Nicolson Become Unstable for Large Time Steps?

AI Thread Summary
The discussion revolves around the stability and accuracy of various numerical differencing techniques for solving the 1D transient heat conduction equation using MATLAB. The Crank-Nicolson method exhibits oscillations around the actual temperature value, while the DuFort method diverges significantly. Concerns are raised about the implementation of these methods, particularly the Backward Euler scheme, which should yield a steady-state solution even with large time steps. Participants emphasize the importance of correctly solving the tri-diagonal matrix involved in the Backward Euler method. Overall, the conversation highlights the challenges of achieving stability in numerical methods for heat conduction problems.
mattyboson12
Messages
38
Reaction score
0
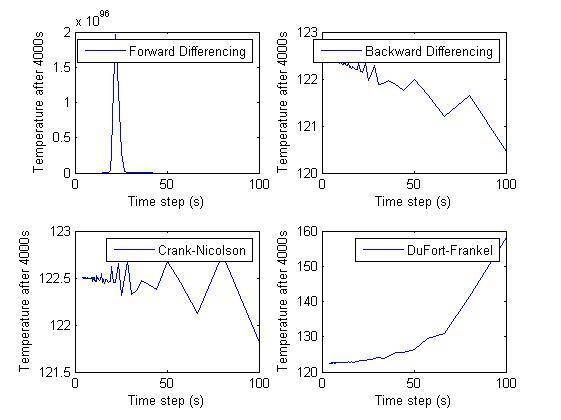
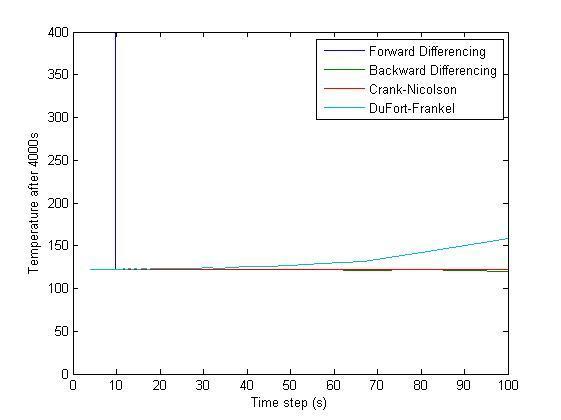
Hi, I have written a MATLAB program to calculate the surface temperature on a tile and I am trying to find the most stable/accurate differenceing technique. I have plotted the surface temperature (where its actual value is ~122.5) against the time step for the differencing techniques shown below. All of them are accurate for small time steps, and then Backwards/DuFort decrease/increase parabolically, is this due to second order accuracy? And why is crank unstable for large timesteps and fowards isn't?

untitled.jpg


untitled1.jpg
 
Physics news on Phys.org
Let's see the PDEs you're solving.

Chet
 
Hi Chet

The program calculates the temperature using fourier's equation in one dimension: dU/dt=α*(d^2 U/d^2 x) . I'm guessing crank is the best method as it seems to have the best compromise between stability/accuracy compared to the others. I am just confused as to why the differencing methods form very distinct graphs ie. why the crank oscillates around the actual value whereas dufort flies off to infinity

kind regards
Matt
 
Based on my experience, you should't be encountering these difficulties solving the 1D transient heat conduction equation using most of these methods. Backward differencing, in particular, should not give rise to the zigs and zags that you are seeing. Are you sure you are implementing these methods correctly? How are you solving for the temperatures at n+1 using your Backward Euler scheme? Are you solving a tri-diagonal matrix?

Chet
 
I've double checked my code and all the methods seem to be okay. Yep, i have used the tri-diagonal matirx and then the built in function tdm() to solve the matrix

Matt
 
Here's something you can check. The Backward Euler method should return the steady state solution after one time step if the time step is made extremely large. Does it? That's an indication of how stable the Backward Euler method is.

Chet
 

Hot Threads

Recent Insights

Back
Top