Why Does Energy Seem to Disappear in a Gyroscopic Wheel Experiment?

[Low-Q]

This is an experiment with gyros on a wheel.

First of all, this is not a homework question - I am just a 40 year old man with general interests in physics.

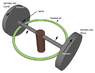
Example: I have a wheel. Attached to its circumference, there are placed heavy discs that is aligned tangentially. These discs are connected to a gear mechanism which will let the discs start spinning fast when the wheel is turned around slowly.

All these discs are now gyros which will resist any change in alignment as they are spinning fast tangentially at the circumference of the wheel.

Initially I must add energy to accelerate the wheel. Now, to maintain a given RPM of the wheel, I must constantly add energy to it, even if friction is not present, because the gyros will try to stop the wheel from turning around.

Where do the input energy go? I ask because in this experiment, I cannot (appearently) get back the energy I add to the wheel except for portions of the energy I added during acceleration. I appearently waste energy that for some reason just disappear. There is no fricton, so there is not generating heat, or other forms of radiation.

Can somebody please explain why it appearently is no conservation of energy in this experiment?

I can make a brief drawing of the experiment if that helps.

Br.

Vidar

 

[Whovian]

The gyroscopes, while trying to minimize friction, still allow for some friction, it's physically impossible to engineer such to have no friction. There's also friction with the surrounding air.

So it's going to heat, which, I'm sorry to tell you, once it's gone into the environment, you can't get out without expending significant energy to do so.

 

[Low-Q]

Here is the drawing. Reminds me of a power ball when I look at it...

 

[Low-Q]

The gyroscopes, while trying to minimize friction, still allow for some friction, it's physically impossible to engineer such to have no friction. There's also friction with the surrounding air.

So it's going to heat, which, I'm sorry to tell you, once it's gone into the environment, you can't get out without expending significant energy to do so.

That was not my point. Read my post again. Conservation of energy, friction etc. is something we all know well about. However, in this thinking experiment there is more than friction that require energy to sustain motion. The gyros will counterforce the rotation of the wheel. Friction will to, but that is not the subject here. This counterforce is made by the gyros, so even if the friction will steal 1Nm of torque, the gyros might steal 100Nm of torque.

So, can you tell me where the energy spent to fight against the gyroscopic counter torque go?

Look at the picture above.

Vidar

 

[Dale]

If I understand your setup correctly then the work goes into increasing the KE of the gyros.

 

[Low-Q]

If I understand your setup correctly then the work goes into increasing the KE of the gyros.

How can KE increase if the system is stable at one given velocity?

The green circle is part of the gear mechanism that makes the gyros to spin. The gyros must orbit the center of the green circle in order to start spinning. But since the gyros resist disalignment, it will require energy to sustain the cycles at the same rate. It has gained KE by the acceleration of mass, and KE will stay constant until the system slows down. Appearently there has been applied more energy into the system than we in theory can get back when the system slows down to a full stop.

That is what I do not understand.

Vidar

 

[TurtleMeister]

Gyroscopes are interesting because they can sometimes be non-intuitive. If you try to rely on your intuition you can possibly be led astray. An example is Eric Laithwaite's famous lecture at the Royal Institution in 1974, where he performed a demonstration and claimed that gyroscopes could be used as a means of reactionless propulsion.

The two gyroscopes in your illustration are rotating in opposite directions. This means that their gyroscopic actions will cancel out (I think this may be where your intuition is leading you astray). If the system is stable at one given velocity then the only energy input required would be for whatever is required to overcome friction.

 

[Low-Q]

Gyroscopes are interesting because they can sometimes be non-intuitive. If you try to rely on your intuition you can possibly be led astray. An example is Eric Laithwaite's famous lecture at the Royal Institution in 1974, where he performed a demonstration and claimed that gyroscopes could be used as a means of reactionless propulsion.

The two gyroscopes in your illustration are rotating in opposite directions. This means that their gyroscopic actions will cancel out (I think this may be where your intuition is leading you astray). If the system is stable at one given velocity then the only energy input required would be for whatever is required to overcome friction.

What if one gyro was spun by the opposite side, so they rotates in the same direction? Or what if one of them was removed?

Other than that, two opposite spinning gyros do not cancel each other out, they apply each other. You must see each gyro as separate working units that resist disalignment.

I'm still clueless of where the applied energy goes - energy just can't disappear or be destroied...

Vidar

 

[TurtleMeister]

Other than that, two opposite spinning gyros do not cancel each other out, they apply each other. You must see each gyro as separate working units that resist disalignment.

Vidar

Wrong.

 

[Dale]

How can KE increase if the system is stable at one given velocity?
...
But since the gyros resist disalignment, it will require energy to sustain the cycles at the same rate.

This is not correct. It does not require work to sustain the precession. What would make you think that?

 

[the_emi_guy]

All these discs are now gyros which will resist any change in alignment as they are spinning fast tangentially at the circumference of the wheel.

Vidar,

When gyroscopes "resist any change in alignment" the resistance they offer is perpendicular to the applied force and the motion. In order for the gyroscope to do work, its force must be in the same direction of some motion. Pushing something in a direction that it cannot move does no work, it is like pushing against a wall.

 

[Low-Q]

Wrong.

Interesting. Thanks! When the gyroscopes spun in the same direction it looked like a see saw. In my thinking experiment there is no see saw movement allowed. I think I must build it and see for myself :-)

 

[Dale]

Low-Q, energy and angular momentum conservation for isolated systems can be derived directly from Newton's laws. Since this system is governed by Newton's laws we know immediately that those conservation laws hold. However, it is always possible to make a system so complicated that you make a mistake analyzing it. That is why it is best to stick with simple systems. If you ever think you find a violation of some conservation law in a complicated system you know immediately that what you have actually found is a failure in your analysis. Let's walk through the analysis of this device.

There are three important axes, let's call axis A the axis of the toothed rim, axis B is the axis of the two disks, and axis C is the axis perpendicular to both axis A and B. As we apply an external torque about A the toothed gears translates that into two equal and opposite torques about B. Those two torques, being equal and opposite, give equal and opposite angular momentum to each disk. Those two angular momenta cancel out, so the net angular momentum of the device is about axis A. When you remove the external torque, then conservation of momentum demands that the angular momentum (about A) remain.

Now, you wanted to analyze the two disks separately, so let's do that also. Let's call the two disks F and G and let's suppose that the gears are set so that the angular momentum of each points outwards. Let's consider the torques when F is pointing to the right. At that instant the angular momentum of F is also to the right, and since F is precessing towards the back it is experiencing a torque about C (directed towards the back). At that same instant the angular momentum of G is to the left, and since G is precessing towards the front it is experinecing a torque about C (directed towards the front). These two torques cancel and result only in a bending moment in the axis. Assuming a sufficiently rigid and elastic material the net assembly shows none of the deceleration you were suggesting.

 

[Low-Q]

Many thanks for the explanation DaleSpam. I suppose I misunderstand the "inner workings" of a gyro. I thought that it was hard (Not impossible) to turn a gyro perpendicular to the rotation plane. I have a bicycle I can test this with. Spinning the frontwheel to high RPM an try to turn the wheel left or right while the bicycle frame remains in the same position. Then I will soon find out if my experiment confirms my thoughts or not.

Thanks again for your explanation.

 

[AlephZero]

I thought that it was hard (Not impossible) to turn a gyro perpendicular to the rotation plane.

That seems like a misunderstanding of what happens. It is "easy" to turn a gyro in any direction, but the "non-obvious" behaviour is that it doesn't turn in the same direction as you apply the force, not that it won't turn at all.

 

[Low-Q]

That seems like a misunderstanding of what happens. It is "easy" to turn a gyro in any direction, but the "non-obvious" behaviour is that it doesn't turn in the same direction as you apply the force, not that it won't turn at all.

My point was however to turn the gyro in the same direction as the applied force - preventing precession using some kind of mechanical guides. That was the attempt to show in the drawing earlier.
Therefor, as the precession is denied, i assumed it would take energy to turn a gyro in the same direction as the applied force, which is prependicular to the rotation plane of the disc/gyro. Such operation I assume will also slow down the gyro, but the toothed rim is forcing the gyros to spin anyways. So I assumed it would recuire energy to do this, and wondered therfor where this applied energy went. However, as you have explained, it will not take energy, so there is no energy that disappears :-)

Vidar

 

[TurtleMeister]

I think I understand now what your point is. It was complicated by your illustration, which is not a good example of what you're asking. You mentioned the power ball in one of your previous posts. I think if you read the Wikipedia page and watch the video you will know where the energy goes to (or comes from).

http://en.wikipedia.org/wiki/Gyroscopic_exercise_tool


This is an interesting little gadget. I may have to get one. :)

 

[Dale]

I have a bicycle I can test this with.

If you want to test the situation in your drawing you will have to get two counter-rotating bicycle wheels mounted on the same axle. That is very different from just one bicycle wheel since one bicycle wheel can be given significant angular momentum, but two counter-rotating bycycle wheels won't have much.

 

[Low-Q]

I will use a more simple example.

I have a modified powerball that is fixed to a concrete floor.
Assume that I can turn the flywheel in it perpendicular to the flywheels rotation. Initially the flywheel does not spin. It starts to spin only when I turn it perpendiculary. If I stop turning it, its spin also stop. A gear mechanism makes sure of this.
So, the flywheel will under all circumstances spin in the vertical plane, and at the same time can turn in the horizontal plane - without exceptions.

I assume I will feel a counterforce as soon as I try to turn the flywheel perpendicular to its rotation, since the flywheel at the same time starts to spin perpendicular to the turn. Is that correct?

Say the flywheel is spinning constant at 10 000 rpm. And it turns around perpendiculary at a constant 60 rpm. If I successfully maintan this constant cycle over time, would that also mean that I have to apply energy to sustain the rpm in the vertical and horizontal plane except for making up for friction?

Vidar

 

[Dale]

If I successfully maintan this constant cycle over time, would that also mean that I have to apply energy to sustain the rpm in the vertical and horizontal plane except for making up for friction?

Based on the above discussion and your knowledge of physics, what would you guess and why? Think about torque and angular momentum. Think about torque and work. Which torques lead to what changes in angular momentum, and which do work, and why?

 

[Low-Q]

Based on the above discussion and your knowledge of physics, what would you guess and why? Think about torque and angular momentum. Think about torque and work. Which torques lead to what changes in angular momentum, and which do work, and why?

1. I would guess it takes energy to sustain the cycle, because the gyro don't want to turn in the same direction as the applied torque (As shown in the youtube video earlier where the two gyros are spinning in the same direction) - but the gyro in the powerball experiment has no other options other than turning in the same direction as the applied force.
Therfor I guess I must do work while turning the gyro around perpendicular to its rotation. (Suppose it is the same as fighting agains the angular momentum - applying energy to do so)

2. Which torques lead to what changes in angular momentum, and which do work, and why?
Not really sure where you're heading with these questions.

Vidar

 

[Dale]

1. I would guess it takes energy to sustain the cycle,

Since that leads to a failure of conservation of energy we know that this guess is wrong.

because the gyro don't want to turn in the same direction as the applied torque (As shown in the youtube video earlier where the two gyros are spinning in the same direction) - but the gyro in the powerball experiment has no other options other than turning in the same direction as the applied force.
Therfor I guess I must do work whileturning the gyro around perpendicular to its rotation. (Suppose it is the same as fighting agains the angular momentum - applying energy to do so)

Why? Why do you think that work must be done in this case? What is the formula for work in angular motion? Does it apply here?

Which torques lead to what changes in angular momentum, and which do work, and why?
Not really sure where you're heading with these questions.

I am just trying to get you to actually analyze the device using sound physical reasoning.

Use this page as a reference
http://en.wikipedia.org/wiki/Torque
Especially the section on The relation to angular momentum and the section on The relation between torque power and Energy

Other sources are
http://en.wikiversity.org/wiki/Torque_and_angular_acceleration

And
http://bolvan.ph.utexas.edu/~vadim/Classes/2011s/linang.pdf
http://www2.cose.isu.edu/~hackmart/torque.pdf

 

[Dale]

Try to analyze it on your own first, but here are some hints.

Spoiler

Assuming a very high gear ratio we can assume that the angular momentum, L, is almost entirely along the axis of the gyroscope. The gearing makes it so that L precesses slowly about a circle. Since L is changing that means that there is a torque according to \tau=\frac{dL}{dt}.

If L is precessing in a horizontal plane then τ is also in the horizontal plane, but 90° "ahead" of L. So τ tends to make L rotate vertically, but L is mechanically constrained to remain in the horizontal plane. Therefore the rotation about the axis of τ is 0°. Therefore according to W = τ θ the work done by the torque that makes the gyroscope precess is 0.

 

[Low-Q]

Try to analyze it on your own first, but here are some hints.

Assuming a very high gear ratio we can assume that the angular momentum, L, is almost entirely along the axis of the gyroscope.

Does "almost entirely along the axis" mean that the gear ratio isn't infinitely high? If the gear ratio was infinetily high, the angular momentum would be entirely along the axis?

I have now learned that precession will slowly turn the gyroscope in the same direction as the gyroscope is spinning. That precession will occour if a force, like gravity, is trying to overturn the gyroscope. Will it be possible to manually force the "precession" the opposite way if the gyro is still spinning the same way as before?
If so, what happens with the speed of the gyro?

Vidar

 

[Dale]

Does "almost entirely along the axis" mean that the gear ratio isn't infinitely high? If the gear ratio was infinetily high, the angular momentum would be entirely along the axis?

Yes.

I have now learned that precession will slowly turn the gyroscope in the same direction as the gyroscope is spinning. That precession will occour if a force, like gravity, is trying to overturn the gyroscope. Will it be possible to manually force the "precession" the opposite way if the gyro is still spinning the same way as before?
If so, what happens with the speed of the gyro?

You can make the precession go either way simply by changing the direction of the external torque. Nothing happens to the speed of the gyro unless there are losses.

 

[Low-Q]

Thanks. I'm much wiser now :-)

 

[Dale]

Excellent! You are welcome.

 

[Low-Q]

Sorry - not finished yet

I would think that the flywheel mass that constantly changes direction, and thus experiences a form of "pseudo" acceleration or G-forces, would require a certain amount of energy in order to do this.
Such as the "Coriolis" effect (Might be incorrectly expressed) of a centrifugal pump. Although the liquid can be returned to the pump input (a loop where the liquid repeats the same cycle), the acceleration of the fluid tangentially to the rotation as it flows away from the center of the pump will still try to prevent rotation. Where does the energy in such a system go? Will the liquid heat up?

Vidar

 

[Dale]

Sorry - not finished yet

No worries. Questions and answers are not rationed here

I would think that the flywheel mass that constantly changes direction, and thus experiences a form of "pseudo" acceleration or G-forces, would require a certain amount of energy in order to do this.

Neglecting losses precession does not require energy in general. This is because the torque is perpendicular to the axis of rotation. Just like a force perpendicular to motion does no work, for the same reason a torque perpendicular to the rotation also does no work. We have analyzed this specifically for your geared gyroscope, but it applies to precession in general.

Such as the "Coriolis" effect (Might be incorrectly expressed) of a centrifugal pump. Although the liquid can be returned to the pump input (a loop where the liquid repeats the same cycle), the acceleration of the fluid tangentially to the rotation as it flows away from the center of the pump will still try to prevent rotation. Where does the energy in such a system go? Will the liquid heat up?

Yes, in this case the system is not frictionless. For fluids, this kind of friction is called viscosity.

 

[Low-Q]

OK, thanks. I just visualized the experiment where I place a red dot on the flywheels circumference. I rotate the flywheel 1 rps, and the flywheel have a circumference of 1 meter. The red dot travels now at 1m/s. If I turn the flywheel perpendicular to its rotation 1 complete turn per second, the red dot will cover a longer distance per revolution of the flywheel, and increase velocity by how much? Do you have an equation for this?

Vidar