Why does my method for calculating this value from...?

[Rijad Hadzic]

Homework Statement

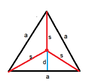
So I have an equilateral triangle of side(s) = 3x10^-2 m

Im trying to find the value of the distance from a point directly in the middle of the triangle, to the middle of one side.

Homework Equations

The Attempt at a Solution

What I wanted to do was, cut the triangle in half, so now I have a hypotenus, of value 3x10^-2 m, a base of half of that, 1.5x10^-2 m, and a side b which I use pythagoras to solve for.

$b = ((3x10^-2)^2 - (1.5x10^-2)^2 ) ^1/2$

which = .02598,

and now taking half of that I have the value of the distance from a point directly in the middle of the triangle, to the middle of one side.

But my book tells me I am wrong.

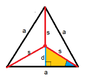
What they did was construct a line from one vertex of the triangle to the middle, then adjacent to that is a line l/2, and then there is another line which I'm trying to solve for, going from the middle of one side to the origin. They then used tan(30) l/2 to calculate it to .0086...

but I don't get why my method works. I'm essentially halfing the equalateral, finding the long side, and taking half of it, how doesn't that give me the value of the distance from a point directly in the middle of the triangle, to the middle of one side

 

[scottdave]

Your definition of center of the triangle is not the same as the book (and what most people consider). Here, it is the center of mass, is essentially what you want to find. If you think about how you cut the triangle into two right triangles, the center of mass will lie on that line where you made the cut, but it will not be the midpoint of that line.
You need to find the point where the area above the point is equal to the area below that point.

 

[ehild]

The centre of the equilateral triangle is at equal distance from all corners of the triangle. In the figure, it is denoted by s. You need to find the distance d.

 

[Rijad Hadzic]

The centre of the equilateral triangle is at equal distance from all corners of the triangle. In the figure, it is denoted by s. You need to find the distance d.
View attachment 213893

I see. So d isn't = to (1/2) s+d, right?

 

[ehild]

I see. So d isn't = to (1/2) s+d, right?

No. d=(1/2)s +d means 0=(1/2)s which is false.
What is the blue angle in the yellow triangle? what is the ratio d/s?

 

[haruspex]

d=(1/2)s +d means 0=(1/2)s

At a guess, Rijad meant d=(½)(s+d), but still false.