Miike012
- 1,009
- 0
Homework Statement
I am reading an explanation on a trig identity but I am not fully understanding it...
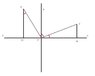
Angle MOP = Theta
Angle POP' = Right angle
Angle AOP' = (Theta + Right angle)
Take OP' = OP ( WHY must it be equal?)
Angle MOP + P'OM' = 90 ( I understand this)
Angle MOP = Angle OP'M' (I understand this)
Both Triangles MOP And M'P'O are equal in all respects (What makes them equal ? Is it because they both have one side equal and an angle that is also equal? And how is this Important to the theorem?)
If these triangle were not "equal in all respects," would this theorem not work?
Then it says... Sin ( right angle plus theta) = cos(theta)
and so on...
I don't understand why Sin ( right angle plus theta) = cos(theta)
Can some one please explain...