SUMMARY
The discussion centers on the Stoke's stream function, specifically its application in fluid dynamics to quantify fluid flow across surfaces of revolution. It establishes that the quantity of fluid crossing the surface formed by the vector OP is represented as 2πc when the position vector is rotated around a reference axis. The analysis further explains that for two closely positioned points P and P', the flow rate across a unit area is quantified as 2πdΨ per unit time, emphasizing the mathematical relationship between the stream function and fluid flow rates.
PREREQUISITES
- Understanding of fluid dynamics principles
- Familiarity with vector calculus
- Knowledge of Stoke's theorem
- Basic concepts of surface integrals
NEXT STEPS
- Study the mathematical derivation of Stoke's stream function
- Explore applications of Stoke's theorem in fluid mechanics
- Learn about surface integrals in vector calculus
- Investigate the implications of fluid flow across surfaces of revolution
USEFUL FOR
Students and professionals in fluid dynamics, mechanical engineers, and researchers focusing on mathematical modeling of fluid flow.
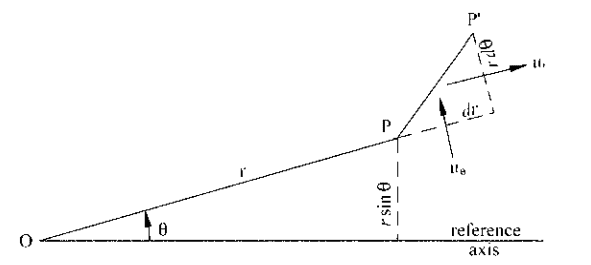
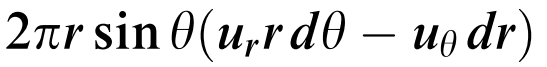 ?
?