Usage of Taylor's formula on stress analysis

[fisher garry]

Moderator Note: Thread moved from forum Atomic, Solid State, Comp. Physic, so no homework template shown.

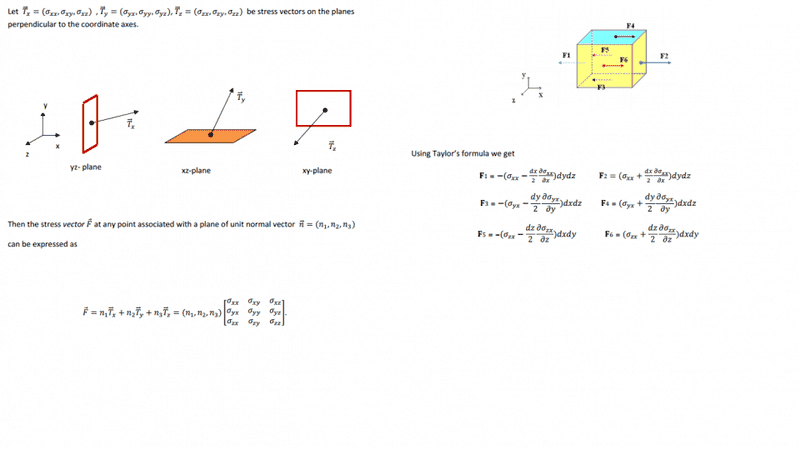
What function do they use Taylor's formula on? And can you show how they derive it? I know how one derives Taylor formula. Thanks! The text i taken from this page:http://ingforum.haninge.kth.se/armin/fluid/exer/deriv_navier_stokes.pdf

 

[Chestermiller]

It isn't clear what you are asking. What exactly do you mean by Taylor's formula? Are you talking about the use of a Taylor series in stress to derive the stress-equilibrium equation?

 

[fisher garry]

It isn't clear what you are asking. What exactly do you mean by Taylor's formula? Are you talking about the use of a Taylor series in stress to derive the stress-equilibrium equation?

They use Taylors formula on the functions $F_1$, $F_2$, $F_3$, $F_4$, $F_5$ and $F_6$. Where do they get the formulas from and show how the Taylors formulas are used on the functions. I only wonder about the mathematical relations not about any understanding of stress-equiibriums.

 

[Chestermiller]

They use Taylors formula on the functions $F_1$, $F_2$, $F_3$, $F_4$, $F_5$ and $F_6$. Where do they get the formulas from and show how the Taylors formulas are used on the functions. I only wonder about the mathematical relations not about any understanding of stress-equiibriums.

They are making use of a truncated Taylor series expansion as follows:$$f\left(x+\frac{\Delta x}{2}\right)=f(x)+f'(x)\frac{\Delta x}{2}$$
$$f\left(x-\frac{\Delta x}{2}\right)=f(x)-f'(x)\frac{\Delta x}{2}$$

Assuming that the stress tensor varies with spatial position, they are finding the components of the forces exerted by the surrounding material on the 2 faces of the little cube that are perpendicular to the x axis. These two faces are located at $x+\Delta x/2$ and at $x-\Delta x/2$, while the center of the cube is at x. So F1 is the normal component of force acting on the face at $x-\Delta x/2$, and F2 is the normal component of force acting on the face at $x+\Delta x/2$. They are doing all this so that they can do a differential force balance on the cube.