Why Does the Electric Field Component Ex Require a Negative Sign?

[yesmale4]

Homework Statement

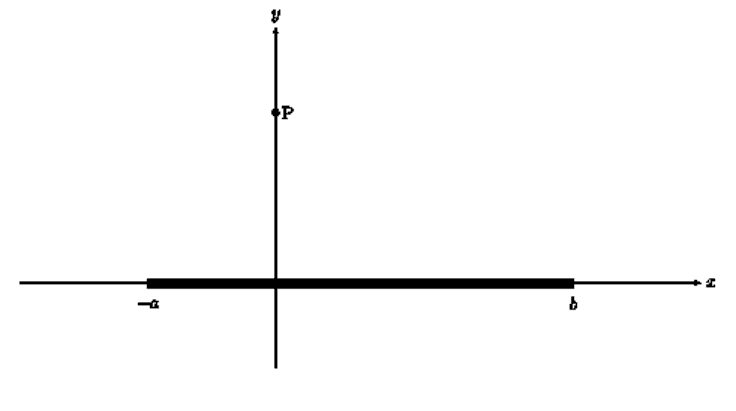
A uniformly charged rod is positioned along the x-axis as shown in the figure. Calculate the electric field at a point P on the y-axis.

Relevant Equations

dq=lamda*dx
de=kdq/r^2

hello i would like to understand to something.
here is the drew

now for my question:
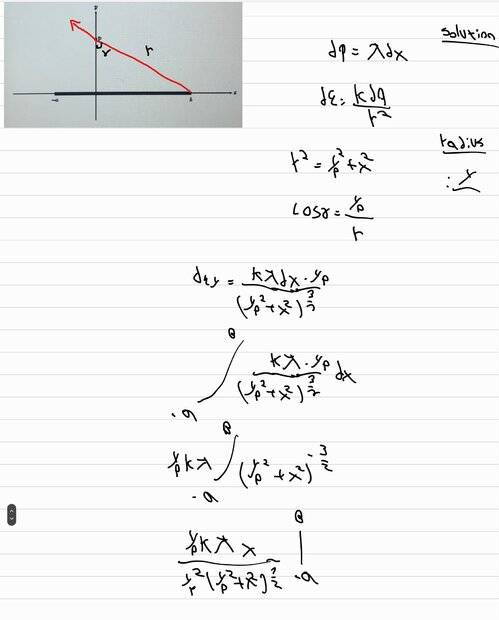
i was able to find Ey and here is my correct answer:

when i try to find Ex i didnt understand something, i found the correct answer but i need to put minus before and i want to know why?
here is my solution for Ex (the correct answer):

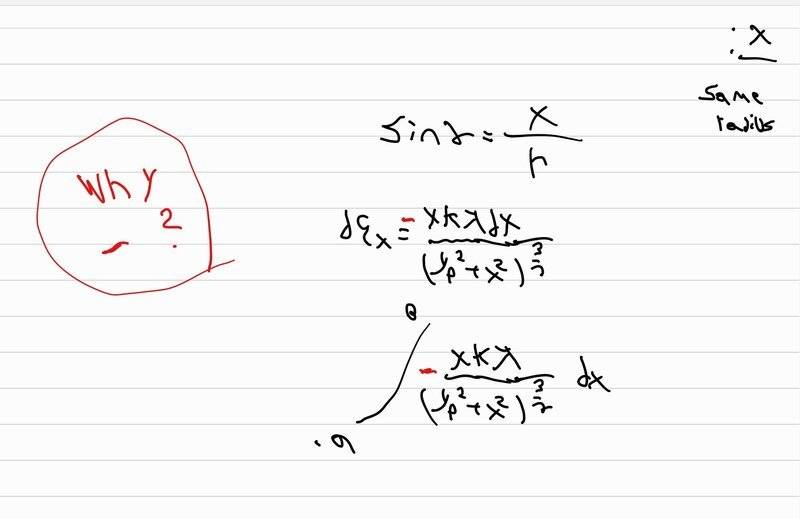
yes i know i didnt solve the integral because first i want to know why there is minus

 

[kuruman]

There is more charge to the right of the vertical line than to the left. The sum of all the contributions from the charge on the right will be grater than the contributions from the charge on the right. So if λ is positive the overall x-component will be negative and the opposite if λ is negative.

Of course, this should be built in the answer. You say that your answer is correct, but how do you know that? It looks like the ends of the rod are at $x=-a$ and $x=\delta,$ Your final answer should have no $x$ in it; only $a$ and $\delta$ and be the sum of two expressions resulting from the integral.

Also, please use LaTeX. Your handwriting is hard to decipher at times.

 

[vela]

when i try to find Ex i didnt understand something, i found the correct answer but i need to put minus before and i want to know why?

What is the sign of the x-component of the arrow you drew?

 

[haruspex]

why there is minus

Because the sign of the x component of the field due to an element dx at x has the sign of $-\lambda x.dx$. I.e. if $\lambda$ is positive then where x is negative the field is to the right and vice versa.

Your final answer should have no x in it

It doesn't really have an x in it - that's just a dummy variable. The OP has merely not done the final step of applying the bounds. Maybe that's what you meant.
And I think it is b, not $\delta$.

 

[kuruman]

It doesn't really have an x in it - that's just a dummy variable. The OP has merely not done the final step of applying the bounds. Maybe that's what you meant.

Yes, that's what I meant. Applying the bounds would yield the difference of two terms in which case it would be easier to point out mathematically that the sign of the x-component depends on both the sign of the linear charge density and the relative size of the bounds.