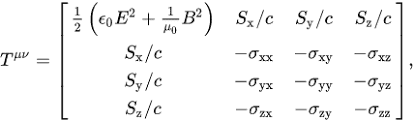A Why Does the Energy-Stress Tensor Exclude Other Forces?

[VictorMedvil]

Hello, I was wondering why the energy-stress tensor only accounts for electromagnetic Energy Density and does not include the other forces? Secondary question could this be a flaw within the mathematics of GR making it give nonsense answers for Quantum level interactions?

 

[PeterDonis]

I was wondering why the energy-stress tensor only accounts for electromagnetic Energy Density and does not include the other forces?

It does include the other forces. The stress-energy tensor includes all stress-energy from all sources. These are not limited to "forces", by which I assume you mean stress-energy density due to fields; stress-energy due to matter is also included.

 

[PeterDonis]

the energy-stress tensor

What you wrote down is not "the stress-energy tensor" without qualification. It is only the stress-energy tensor due to electromagnetic fields.

 

[VictorMedvil]

What you wrote down is not "the stress-energy tensor" without qualification. It is only the stress-energy tensor due to electromagnetic fields.

Okay thanks that clears that up, what is the other version of the Energy-Stress tensor look like?

 

[PeterDonis]

what is the other version of the Energy-Stress tensor look like?

It depends on what kinds of sources are present. There is no single "version" that covers all cases.

 

[VictorMedvil]

It depends on what kinds of sources are present. There is no single "version" that covers all cases.

Okay Thanks PeterDonis.

 

[VictorMedvil]

It does include the other forces. The stress-energy tensor includes all stress-energy from all sources. These are not limited to "forces", by which I assume you mean stress-energy density due to fields; stress-energy due to matter is also included.

Yes, and I did mean due to fields but there is no "any case" it just depends on the Stress sources exactly what I wanted to know .

 

[Orodruin]

Yes, and I did mean due to fields but there is no "any case" it just depends on the Stress sources exactly what I wanted to know .

The most general form (or definition) of the stress-energy tensor in GR is
$$
T_{\mu\nu} = \pm \frac{2}{\sqrt{|\bar g|}} \frac{\delta \mathcal S}{\delta g^{\mu\nu}},
$$
where $\pm$ depends on your sign conventions, $\bar g$ is the metric determinant, and $\mathcal S$ is the action for what you are computing the stress-energy tensor for (ie, not including the Einstein-Hilbert part of the action).

 

[vanhees71]

It does include the other forces. The stress-energy tensor includes all stress-energy from all sources. These are not limited to "forces", by which I assume you mean stress-energy density due to fields; stress-energy due to matter is also included.

No, that's the energy-momentum tensor of the electromagnetic field only. The total energy-momentum tensor also has to include the "mechanical" part of the charges. Only the total energy-momentum tensor is conserved!

One model for an energy-momentum tensor for the charges is that of an ideal fluid,
$$T_{\text{mech}}^{\mu \nu} = (U+P) u^{\mu} u^{\nu} -P \eta^{\mu \nu},$$
where $U$ and $P$ are the internal energy density and pressure as measured in the local rest frame of the fluid, and $u^{\mu}=u^{\mu}(x)$ is the four-velocity flow field in units of $c$, i.e., normalized such that $u_{\mu} u^{\mu}=1$.

 

[Orodruin]

No, that's the energy-momentum tensor of the electromagnetic field only. The total energy-momentum tensor also has to include the "mechanical" part of the charges.

I think you are misreading Peter’s post.

 

[PeterDonis]

No, that's the energy-momentum tensor of the electromagnetic field only.

I'm not sure why you quoted me for this response; you are saying the same thing I was saying.

 

[PeterDonis]

The total energy-momentum tensor also has to include the "mechanical" part of the charges.

It also has to include stress-energy that might have nothing whatever to do with charges at all.

 

[vanhees71]

I'm not sure why you quoted me for this response; you are saying the same thing I was saying.

Obviously it was a misunderstanding, because you wrote "It does include the other forces. The stress-energy tensor includes all stress-energy from all sources." What's written in #1 is the em. part only, as far as I read this expression.

 

[vanhees71]

It also has to include stress-energy that might have nothing whatever to do with charges at all.

Of course, that's what the energy-momentum tenor is (perhaps one should rather call it energy-momentum-stress tensor, because the space-space components are the usual stress tensor also known in non-relativistic continuum mechanics).

That's also clear when looking at the most simple case of an ideal fluid, where
$$T^{\mu \nu} = (U+P) u^{\mu} u^{\nu} - P g^{\mu \nu}$$
(in west-coast convention for the metric). Indeed it contains both the internal energy and the stress (pressure) in the expression for the energy density, which is $T^{00}$.