Why Does the Projection of a Jinc Result in a Sinc?

[Wxfsa]

It basically boils down to:
show that:
$$\int_{-\infty}^{\infty} dy \frac{J_1 \left ( \pi\sqrt{x^2+y^2} \right )}{\sqrt{x^2+y^2}} = \frac{2 \sin{\pi x}}{\pi x} $$

My life story (somewhat irrelevant):
A jinc function is besselj(1,pi*r)/( 2r ), a sinc is sin(pi*x) / (pi*x)
I have noticed, while doing numerical work, that if I took the line integral of a jinc (which is a 2D function of r=sqrt(x^2+y^2)), I'll get exactly a sinc

The exact expression was:

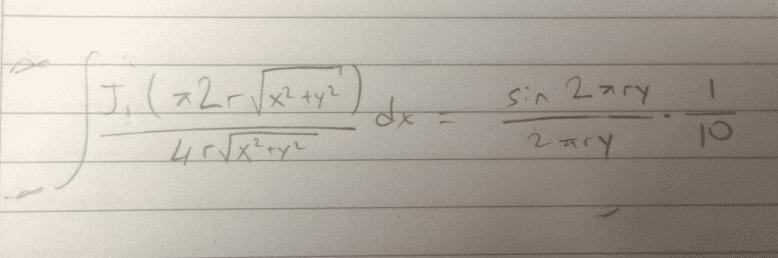
please assume that "r" in that expression is just some constant. in fact, 1/10 on the right side should be 1/(2r)

I don't really care about something exact, I just want to see why a line integral through a J1(r)/r has the form sin(y)/y

I tried writing the bessel function in the integral form and then change the order of integration but i don't see a way. I am hoping someone already knows the answer here.

    p=0.01:0.01:0.5;
    result1=zeros(1,length(p));
    result2=zeros(1,length(p));
    r=3;
    f= @(u,v) besselj(1,pi*2*r*sqrt(u.^2+v^2))./(4*r*sqrt(u.^2+v^2));
    res = @(v) sinc(2*r*v)/2/r;%1/2/r *besselj(1,pi*2*r*v)./(4*r*v);

    for i = 1:length(p)
        v=p(i);
        result1(i)=2*integral(@(u)f(u,v),0,1000);
        result2(i)=res(v);
    end
    figure
    hold on
    plot(result1,'b')
    plot(result2,'r')

this is the MATLAB code if anyone is interested, mathematica could not do it.

 

[Wxfsa]

http://math.stackexchange.com/questions/1221767/a-bessel-function-integral