B Why Does This Number Pattern Always Result in 6?

[snshusat161]

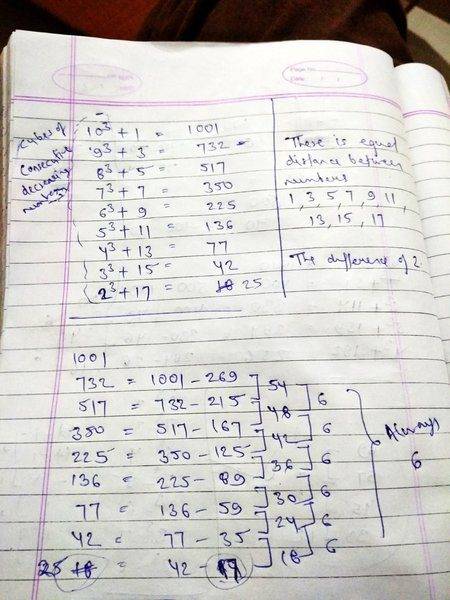
I was just playing with some numbers and I noticed this weird pattern. Because of the complexity of the problem I am finding it hard to describe it in words. But you can easily understand it by looking at the picture. Whenever I form a series by adding numbers in Arithmetic progression to the cubes of consecutively decreasing numbers then they always give 6 if I follow the steps shown in the pic. There must be some reason behind it. Can anybody help me find it. I am just asking it out of curiosity.

 

[cosmik debris]

Look up the method of finite differences.

Cheers