I Why is E(t) multiplied by e^(-ix) in Plancherel's Theorem proof?

[QuantumDuality]

the first step of the Plancherel's Theorem proof found in: http://mathworld.wolfram.com/PlancherelsTheorem.html, says:
let

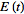be a function that is sufficiently smooth and that decays sufficiently quickly near infinity so that its integrals exist. Further, let

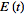and

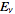be FT pairs so that:

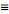
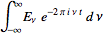
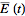
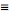
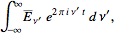
assuming x = 2*pi*v*t, why is E(t) multiplied by e^(-ix)?, i guess it has to do with the fact that it is the conjugate of e^(ix), but i can't figure it out

 

[Delta2]

The first equation follows from the definition of Fourier Transform pairs (to be more precise from a theorem that the inverse Fourier transform of the Fourier transform of a function, is the function itself).

The second equation follows from first by taking the complex conjugate at each side of the first equation. And of course changing the name of the variable but I guess you know that $\int f(x)dx=\int f(y)dy$ no matter what x and y are.

 

[QuantumDuality]

but if we have for example:
f(x) = x³
y = x²
then
f(y) = (x²)³ = x⁶
dy/dx = 2x
dy = 2x dx

using the equation you suggest:
∫f(x)dx=∫f(y)dy
∫x³ dx=∫2x⁷ dx

i'm missing something?

 

[Delta2]

Well the equation I wrote is for definite integrals (ok I admit I didn't write it in an accurate way) , so i should ve write $\int\limits_{a}^{b}f(x)dx=\int\limits_{a}^{b}f(y)dy$

What you doing is a change of variable $y=x^2$ in the integral $\int\limits_{a}^{b}f(y)dy$ so the interval of integration changes from $(a,b)$ to $(\sqrt{a},\sqrt{b})$. So the last line of your post should be actually $\int\limits_{a}^{b}x^3dx=\int\limits_{\sqrt{a}}^{\sqrt{b}}2x^7dx$.