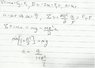Why Is My Solution for Rotational Motion Incorrect?

AI Thread Summary
The discussion centers on a student's confusion regarding an incorrect solution for a rotational motion problem. The student made an error by improperly canceling variables in their equation, leading to a different answer. Other participants emphasize that such algebraic mistakes are common and encourage careful review of work to avoid them. They share experiences of even experienced professionals making similar errors. Overall, the conversation highlights the importance of meticulousness in solving physics problems.
GreenPrint
Messages
1,186
Reaction score
0

Homework Statement



Please see the attachment.

Homework Equations





The Attempt at a Solution



Please see the attachment. When I tried to solve the equations for a I got a different answer and I don't see what I'm doing wrong. Please let me know if you cannot follow my work. Thanks for any help you can provide.
 

Attachments

  • Untitled.png
    Untitled.png
    37.3 KB · Views: 408
  • Scan3.jpg
    Scan3.jpg
    45.9 KB · Views: 379
Physics news on Phys.org
Illegal algebra cancellation.

\frac{MR^2}{2}\frac{a}{r}=(F_T)\,r

In the above equation, you canceled r on the left side with r on the right side.
 
oh that's embarrassing thanks
 
GreenPrint said:
oh that's embarrassing thanks

Don't be embarrassed by it. Arithmetic and algebraic mistakes just plumb happen even to the best of us. I've had a professor who was the chair of my university's physics department and who performs nuclear physics experiments (specifically with lead nuclei, IIRC) at the LHC, and on occasion he made algebra errors when demonstrating examples on the board. Just go through stuff more slowly and carefully, and you should minimize the number of those mistakes that you make. :)
 
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanged mass'

Thread 'A cylinder connected to a hanged mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Motion of Sphere Rolling Down Rotating Cone
Replies
9
Views
2K
Question about springs and rotational/translational energy
Replies
4
Views
1K
Coordinates of a point on a rotating wheel
Replies
3
Views
2K
Rotational Motion Problem with Varying Centripetal Force and Friction
Replies
10
Views
2K
Is the Solution for Rotation of Spherical Mirrors Incorrect?
Replies
16
Views
1K
Oscillatory motion problem: Bicycle wheel rotation oscillation
Replies
17
Views
887
Why can't I treat the disk as a point mass?
Replies
3
Views
1K
Atwood's with a cylinder - Rotational Motion
Replies
13
Views
832
Circular motion of a rotational spring
Replies
12
Views
3K
How Does Coriolis Force Influence Particle Motion in Rotating Systems?
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top