tonyza2006
- 3
- 0
Hi there,
I don't understand why the equal of Newton's law of gravitation F = Gm1m2/d(squared) is different for no spherical objects.
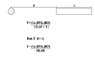
In the image of my attachment there are one spherical object and a no spherical object. So why if there are not very distant the equal used is F = Gm1m2/d(d+L).
How It's used (d).(d+L) on the contrary (d).(d), which is the original equal?
Thanks
Tony
PS: Sorry about my english.
I don't understand why the equal of Newton's law of gravitation F = Gm1m2/d(squared) is different for no spherical objects.
In the image of my attachment there are one spherical object and a no spherical object. So why if there are not very distant the equal used is F = Gm1m2/d(d+L).
How It's used (d).(d+L) on the contrary (d).(d), which is the original equal?
Thanks
Tony
PS: Sorry about my english.