B Why is the force pushing electrons downwards in this scenario?

[Saracen Rue]

Hello Physics Forums users,

Thank you for taking the time to read my thread. I has just reading through this following article: http://www.sciencehq.com/physics/electromagnetic-induction.html when I came across this:

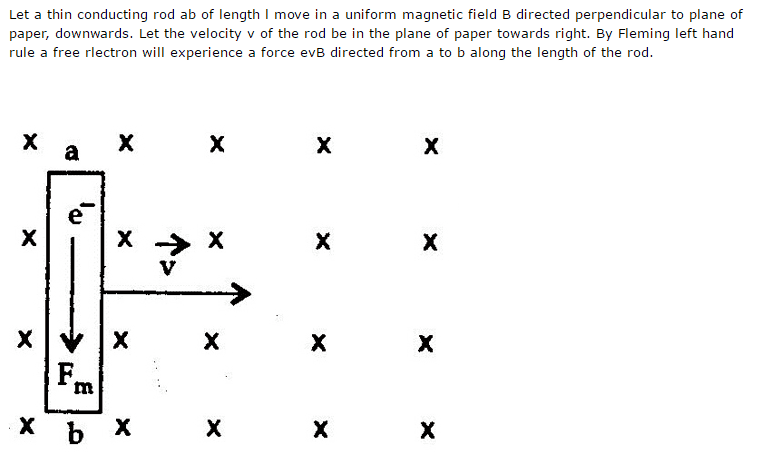
And became rather confused. The right hand rule dictates that in this scenario; positive particles moving towards the left through a magnetic field into the page should result in a force that acts upwards. Due to the fact that electrons are the only free-moving component inside a metallic lattice, they should be forced upwards. However, this article states that the force pushes them downwards. Any help with understanding what's happening here is much appreciated.

Again, thank you for your time :)

 

[JoePhysics]

Remember that $\mathbf{F} = q \mathbf{v} \times \mathbf{B}$. By the right-hand rule, $\mathbf{v} \times \mathbf{B}$ is a vector that points up in this scenario, and since $q$ is negative (it is the charge of the electron), you know the rest.

 

[Saracen Rue]

Ah thank you very much, that makes a lot more sense now. The right hand rule isn't indicating the direction of the force but rather the direction of vector $v*B$.

Again, thank you for your help! :)

 

[JoePhysics]

Ah thank you very much, that makes a lot more sense now. The right hand rule isn't indicating the direction of the force but rather the direction of vector $v*B$.

Again, thank you for your help! :)

You're welcome!

Just a clarification, the vector we're looking at is $\mathbf{v} \times \mathbf{B}$. What you wrote, $v*B$, seems like the product of their lengths.