Why is the Mercury Displacement Different in the Left Arm of the Tube?

[vcc]

There is a question that I have been stumped on for a while now.

it is as follows:

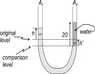
"The left arm of a tube has a corss sectional area A1 of 10.0cm^2 and the right arm has a cross sectional area of A2 = 5.00cm^2.

100g water are poured into the right arm.

b) givent he density of mercury is 13.6g/cm^3, what distance 'h' does the mercury rise in the left arm?

I worked out in question 'a' that the length of the column of water is 20cm.

With this, I used Pnot + densityofmercury*g*Hmercury = Pnot + densityofwater*g*Hwater

This gives me the Hmercury displaced on the right arm.

With that displacement, which I calculated to be Hmercury = 1.47cm, I can calculate the displacement on the left side.

V1=A1H1 <volume of displacement1\____should be equal
V2=A2Hmercury <volume of displacement2/

V1 = V2

therefore A2(1.47cm)/A1 = H1

I calculated H1 to be 0.735cm or 7.3mm

However, this answer is wrong. THe correct answer is 4.9mm

Why is this?? I am truly frustrated and stumped

 

[vcc]

I'd appreciate some form of a reply. That way I know what to change in the phrasing of the above post.

 

[andrevdh]

I have tried my hand at it for more than an hour - no luck yet - got it ! It needs a detailed drawing which takes some time to approve so here goes...
The general idea is still to compare the pressures in the two arms at the height of the bottom of the water column. The height of the displaced mercury volume $\Delta V$ in the right arm comes to
$$h'=h\frac{A_1}{A_2}$$
the height of the column in the left arm that we want to compare with the water column is then given by
$$h+h'$$
comparing the pressures then gives $h$.

 

[vcc]

I have tried my hand at it for more than an hour - no luck yet - got it watch this space - it needs a detailed drawing which takes some time to aprove so here goes...
The general idea is still to compare the presure in the two arms at the height of the bottom of the water column. The height of the displaced mercury volume $\DeltaV$ in the right arm comes to
$$h'=h\frac{A_1}{A_2}$$
the height of the column in the left arm that we want to compare with the water column is then given by
$$h+h'$$
comparing the pressures then gives $h$.

Thanks for the help and effort btw. I appreciate it