- #1
Queren Suriano
- 50
- 0
Homework Statement
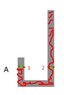
A J-shaped tube has an uniform cross section and it contains air to atmosphere pression of 75 cmo of Hg. It is pours mercury in the right arm, this Compress the closed air in the left arm. Which is the heigh of the mercury's column in left arm when the right arm is full of mercury? Consider that in every moment temperature is constant and that the air is an ideal gas. Consider h1 = 0.25m and h2 = 2.25m
2. Relevant equations
P= Patm + density*g*h
P1*V1 = P2*V2
The Attempt at a Solution
I have equalized the pressure at point 1 with the pressure at point 2, and this looks like this:
Pressure at point 1 = Air density * gravity * (0.25-h)
Pressure at point 2 = Atmospheric pressure + mercury density * gravity* (2.25-h)
The atmospheric pressure I suppose is 75 cm Hg.
From previous equations I would solve for "h"
My question is if the approach is right? and how I could consider the density of the air?
Could I solve the problem by applying theory of ideal gases? thanks for your help