Why is the momentum not conserved

[Probie1]

Homework Statement

Two vehicles collide one has a velocity of .0246 m/s the other a velocity of 4.374 m/s at impact. After impact one has a velocity of .49 m/s and the other a velocity of .91 m/s.

Homework Equations

(p) = mv

The Attempt at a Solution

(p)1 = 13158 * -0.0246
(p)1 = -323.68

(p)2 = 1726 * 4.374
(p)2 = 7549.52

at impact momentum = 7225.84 = (p)1 + (p)2

(p)3 = 13158 * -0.49
(p)3 = -6447.42

(p)4 = 1726 * 0.91
(p)4 = 1570.66

after impact momentum = -4876.76 = (p)3 + (p)4

So Iam missing 12102.6 kg*m/s. Why is this like this...am I missing something?

 

[cepheid]

Your problem statement doesn't actually pose a question. It is literally just a statement.

It also doesn't give the mass of either vehicle. So we have no way of knowing if the masses you assumed are what was intended.

It also doesn't give any directions. Are the two vehicles initially traveling in the same direction or opposite directions?

Basically, we don't have the info we need to evaluate if your work is sensible or not.

 

[Probie1]

Sorry about that

Two vehicles collide one has a velocity of .0246 m/s the other a velocity of 4.374 m/s at impact. After impact one has a velocity of .49 m/s and the other a velocity of .91 m/s.



veh1

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 ms
departure velocity 0.49 ms

veh2

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 ms
departure velocity 0.91 ms


Veh 2 is heading toward veh1 slightly off of 180 deg.

 

[gneill]

Momentum is a vector quantity. Compute the separate components of the momentum for each vehicle both before and after collision. What's the total momentum vector before? After?

 

[Probie1]

Okay,

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 ms
departure velocity 0.49 ms

Momentum-in Veh1

p = mv
p= 13158 * 0.0246
p = 323.68

Out

p = mv
p= 13158 * 0.49
p = 6447.42


veh2

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 ms
departure velocity 0.91 ms

Momentum-in Veh2

p = mv
p= 1726 * 4.374
p = 7549.52

Out

p = mv
p= 1726 * 0.91
p = 1570.66

The total before is 7873.2 and after is 8018.08

okay, but I still see a difference in momentum. Am I to include the approach and departure anges in this as well?

 

[gneill]

okay, but I still see a difference in momentum. Am I to include the approach and departure anges in this as well?

Of course! Momentum is a vector: it has both magnitude and direction; it has components.

Compute the momentum vector components for the vehicles before and after. Find the total momentum vector components for before and after. Then compare them.

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 ms
departure velocity 0.49 ms

Momentum-in Veh1

p = mv
p= 13158 * 0.0246 * (sin 0 = 0)
p = 0

Out

p = mv
p= 13158 * 0.49 * (sin 179 = .017)
p = 109.60



veh2

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 ms
departure velocity 0.91 ms

Momentum-in Veh2

p = mv
p= 1726 * 4.374 * (sin 190 = -0.173)
p = -1306.06

Out

p = mv
p= 1726 * 0.91 * (sin 245 = -0.906)
p = -1423.01

Well... this is big time messed up.

 

[gneill]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 ms
departure velocity 0.49 ms

Momentum-in Veh1

p = mv
p= 13158 * 0.0246 * (sin 0 = 0)
p = 0

That's the y-component. What happened to the x-component? Your collision is happening the the x-y plane, so vectors will have x and y components.

Out

p = mv
p= 13158 * 0.49 * (sin 49 = .754)
p = 4803.32

Again, there should be both x and y components. And where did this angle "49" come from?
I thought the "departure" angle was 179°?

So you still need to sort out the rest of the vector components...

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 ms
departure velocity 0.49 ms

Momentum-in Veh1

p = mv
p= 13158 * 0.0246 * (sin 0 = 0)
p = 0

Out

p = mv
p= 13158 * 0.49 * (cos 179 = -0.999)
p = -6446.43



veh2

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 ms
departure velocity 0.91 ms

Momentum-in Veh2

p = mv
p= 1726 * 4.374 * (sin 190 = -0.173)
p = -1306.06

Out

p = mv
p= 1726 * 0.91 * (cos 245 = -0.422)
p = -662.81

The 49 was just a idiot mistake.

 

[gneill]

Still waiting to see ALL the components for ALL the momenta. For example, I see a calculation for the y-component of the momentum of the first vehicle for before the collision, but I don't see the corresponding x-component... and I see an x-component calculation for the first vehicle's momentum after the collision, but I don't see its y-component...

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 ms
departure velocity 0.49 ms

Momentum-in Veh1

p = mv
p= 13158 * 0.0246 * (sin 0 = 0)
p = 0

Out

p = mv
p= 13158 * 0.49 * (sin 179 = 0.017)
p = 112.52



veh2

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 ms
departure velocity 0.91 ms

Momentum-in Veh2

p = mv
p= 1726 * 4.374 * (cos 190 = -0.98)
p = -7398.53

Out

p = mv
p= 1726 * 0.91 * (cos 245 = -0.422)
p = -662.81



Sorry this is taking so long to grasp.

 

[gneill]

Let's concentrate on one particular vector to begin with; How about the initial momentum of the first vehicle?

You've got the:

vehicle mass: m1 = 13158 kg
Speed: v1 = 0.0246 m/s (meters per second --- you had written ms, which is meter seconds)
direction: θ = 0°

The speed is not a velocity; Speed has magnitude but no direction. Velocity has both magnitude AND direction. You're given the direction angle for the velocity, so you can determine the TWO components (x and y) for the velocity, and hence the TWO components for the momentum.

What are the x and y components of the momentum for the vehicle?

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s


P1x = m1v1 cos 0 = 13258kg * 0.0246 * 1 = 323.68 kg*m/s
P1y = m1v1 sin 179 = 13158kg * 0.49 * 0.017 = 109.60 kg*m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s

P2x = m2v2 cos 190 = 1726kg * .91 * -0.984 = -1545.52 kg*m/s
P2y = m2v2 sin 245 = 1726kg * 4.374 * -.906 = 1731.28 kg*m/s

I am confused about the x and y ...is the approach of each vehicle on the x and then the seperations on the y or is one veh totally y and the othe totally x ?

 

[gneill]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s


P1x = m1v1 cos 0 = 13258kg * 0.0246 * 1 = 323.68 kg*m/s
P1y = m1v1 sin 179 = 13158kg * 0.49 * 0.017 = 109.60 kg*m/s

Er, no. The initial velocity has only one angle, namely 0°. The angle 179° pertains to a different velocity, the departing velocity. We're only concerned with the initial velocity here.

Use 0° for BOTH the x and y component calculations for the initial velocity.

I am confused about the x and y ...is the approach of each vehicle on the x and then the seperations on the y or is one veh totally y and the othe totally x ?

A vector in the plane has two components: an x-direction component and a y-direction component. Every velocity in the plane thus has two components. There is ONE angle associated with a given velocity; it's generally the angle between the velocity vector and the positive x-axis. Use that ONE angle to determine BOTH components for that velocity.

If V is the speed and θ is the angle, then Vx = V cos(θ) and Vy = V sin(θ).

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

Vx = .0246 * cos 0 = .0246
Vy = .49 * sin 179 = .0085

 

[gneill]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

Vx = .0246 * cos 0 = .0246
Vy = .49 * sin 179 = .0085

No! The initial velocity HAS ONLY ONE ANGLE. Forget the 179° for now. That comes later, after the collision. Only the 0° angle exists at the moment. An object cannot be heading in two directions at the same instant in time!

The initial velocity of the first vehicle has one angle: zero degrees. That's the ONLY ANGLE!

The initial velocity vector is comprised of two components: One is its x-component, and one is its y-component. The ONE ANGLE along with the magnitude (speed) define the two components. There is the component that is parallel to the x-axis, and the component that is parallel to the y-axis. Use the trig functions cos and sin to extract those two components USING THE SAME ANGLE.

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

Vx = .0246 * cos 0 = .0246
Vy = .49 * cos 0 = .49

 

[gneill]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

Vx = .0246 * cos 0 = .0246
Vy = .49 * cos 0 = .49

Why are you using the speed from AFTER the collision? Why are you using the cosine function for both components? You want to find BOTH components of the INITIAL velocity (before the collision) for the first vehicle. The initial velocity has ONLY speed 0.0246 m/s at angle 0°. That's all. No other angles or speeds should enter into consideration here.

Perhaps you are unfamiliar with the use of vectors? In the following diagram a velocity vector V is shown on a set of Cartesian coordinate axes. The velocity vector has magnitude |V| which corresponds to the speed, angle θ with respect to the positive x-axis, and x and y components are depicted in red. Use the appropriate trig function of the angle to extract the individual x and y components of V.

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



Vx = .0246 * cos 0 = .0246
Vx = 4.374 * cos 190 = -4.30

Vy = .49 * sin 179 =0.008
Vy = .91 * sin 245 = -0.824

 

[gneill]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



Vx = .0246 * cos 0 = .0246
Vx = 4.374 * cos 190 = -4.30

Those would be the x-components of the initial velocities of vehicles 1 and 2. You should give them distinctive variable names in order to distinguish between them. Something like V1x and V2x.

Now, where are the initial y-components of those same velocities?

Vy = .49 * sin 179 =0.008
Vy = .91 * sin 245 = -0.824

Those are the y-components of the final velocities of the of vehicles 1 and 2. You should give them distinctive variable names in order to distinguish between them. Something like U1y and U2y.

Now, where are the final x-components of these same velocities?

 

[Probie1]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



V1x = .0246 * cos 0 = .0246
V2x = 4.374 * cos 190 = -4.30
V3x = .49 * cos 179 = -0.489
V4x = .91 * cos 245 = -0.384


V1y = .0246 * sin 0 = 0
V2y = 4.374 * sin 190 = -0.759
V3y = .49 * sin 179 =0.008
V4y = .91 * sin 245 = -0.824

 

[gneill]

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



V1x = .0246 * cos 0 = .0246
V2x = 4.374 * cos 190 = -4.30
V3x = .49 * cos 179 = -0.489
V4x = .91 * cos 245 = -0.384


V1y = .0246 * sin 0 = 0
V2y = 4.374 * sin 190 = -0.759
V3y = .49 * sin 179 =0.008
V4y = .91 * sin 245 = -0.824

Okay, I suppose that sorts out all the components. NOTE: you should probably keep an extra decimal place or two in the values of intermediate results to minimize truncation and rounding errors in further calculations.

Now you should be in a position to write the components of the momenta by multiplying the velocity components by the appropriate masses (p = mv).

 

[Probie1]

I hope you mean drop everything before the = sign then multiply the weight with everything after the = sign?



weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



V1x = 13158 * .0246 = 323.6868
V2x = 1726 * -4.30 = -7421.8
V3x = 13158 * -0.489 = -6434.262
V4x = 1726 * -0.384= -662.784



V1y = 0
V2y = 1726 * -0.759 = -1310.034
V3y = 13158 * 0.008 = 105.264
V4y = 1726 * -0.824 = -1422.224

I have to pack it in for the night... thanks for now, will be here tomorrow.
You are the greatest...

Thanks A LOT :)

 

[gneill]

I hope you mean drop everything before the = sign then multiply the weight with everything after the = sign?



weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



V1x = 13158 * .0246 = 323.6868
V2x = 1726 * -4.30 = -7421.8
V3x = 13158 * -0.489 = -6434.262
V4x = 1726 * -0.384= -662.784



V1y = 0
V2y = 1726 * -0.759 = -1310.034
V3y = 13158 * 0.008 = 105.264
V4y = 1726 * -0.824 = -1422.224

After multiplying velocities by mass you get momenta, so you should change the names of the variables accordingly. So, P1y, P2y, P3y,... and so on.

I have to pack it in for the night... thanks for now, will be here tomorrow.
You are the greatest...

Thanks A LOT :)

No worries. Pleasant dreams.

 

[Probie1]

Okay... changed everything to momenta (P)

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s



P1x = 13158 * .0246 = 323.6868
P2x = 1726 * -4.30 = -7421.8
P3x = 13158 * -0.489 = -6434.262
P4x = 1726 * -0.384= -662.784


P1y = 0
P2y = 1726 * -0.759 = -1310.034
P3y = 13158 * 0.008 = 105.264
P4y = 1726 * -0.824 = -1422.224

 

[gneill]

So now calculate the total momentum vectors (before and after). Sum the like-components.

 

[Probie1]

Oh, Oh... I forget which is before and which is after. I have tried different combinations but nothis seems right. (I will say it for you ..."IDIOT".)

 

[Probie1]

Wait... the light just came on... I got it figured out.

P1x = 13158 * .0246 = 323.6868
P2x = 1726 * -4.30 = -7421.8
P3x = 13158 * -0.489 = -6434.262
P4x = 1726 * -0.384= -662.784


P1y = 0
P2y = 1726 * -0.759 = -1310.034
P3y = 13158 * 0.008 = 105.264
P4y = 1726 * -0.824 = -1422.224


(P)in = P1x+P2x+P1y+P2y
(P)in = -8408.1472 kg*m/s


(P)out = P3x+P4x+P3y+P4y
(P)out = 8414.006 kg*m/s

I do hope this is right.

Wow... I imagine that the difference is in rounding of the digits... because you can not gain momentum after a collision.

 

[gneill]

No, it's not correct. You cannot add (in that fashion) unlike components; they are vector components. Thus you cannot arithmetically add x components to y components in that fashion. They must be kept separate. You should end up with separate x and y components for the momentum vectors.

They can be combined into magnitude and angle form by employing a bit of Pythagoras:

$|P| = \sqrt{p_x^2 + p_y^2}~~~~~~~~~~~~~~\theta = tan^-1(y/x)$

Watch out for the quadrant of the angle... the arctan function only returns angles in the first and fourth quadrants, so use a bit of thought to place the quadrant using the signs of the individual x and y components. A better choice of function is the atan2(y,x) function which handles all of this automatically, and which you may or may not have on your calculator, or it may have a built in rectangular-to-polar mechanism.

 

[Probie1]

x = -14195.1592
y = -2626.994

P=√(Px^2 + Py^2)
P = 14436.19209

I'm not sure about this other thing
θ=Tan-1(y/x)
θ= 10.48

 

[gneill]

x = -14195.1592
y = -2626.994

P=√(Px^2 + Py^2)
P = 14436.19209

I'm not sure about this other thing
θ=Tan-1(y/x)
θ= 10.48

I can't tell where your x and y values have come from, nor can I tell which particular momentum vector they're supposed to represent.

Let's start by clearing up the initial momentum. Forget the 'departure' values for a moment.
Write the initial momenta of the two vehicles in component form:

p1o = xxxx i + yyyy j

p2o = xxxx i + yyyy j

where i and j designate the vector x and y unit vectors.

 

[Probie1]

At this point I am lost completely... I have no clue what I am suppose to do.

 

[gneill]

At this point I am lost completely... I have no clue what I am suppose to do.

You want to start by making a clear distinction between initial values and final values. So far you've been mixing all the parts in various places in your calculations. This leads to confusion.

So start by taking your initial values for the two vehicles and writing the momentum vector components for each. You've already done the calculations of the values, but they haven't been organized in such a way that they are clear to work with. The format that I showed in my last post is a convenient way to display them. You will have two vectors written in the form xxxxx i + yyyyy j, where xxxxx is the x-component value and yyyyy is the y component value.

Then we can combine these two vectors to find the total initial momentum. After that, we'll do the same for the final values. The results can then be directly compared.

 

[Probie1]

Okay let's try again.

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s

*V1ix = in V1ox = out


V1ix = 13158 * .0246 = 323.6868
V2ix = 1726 * -4.30 = -7421.8
V1ox = 1318 * -0.489 = -6434.262
V2ox = 1726 * -0.384 = -662.784


V1iy = .0246 * sin 0 = 0
V2iy = 1726 * -0.759 = -1310.034
V1oy = 13258 * 0.008 = 105.264
V2oy = 1726 * -0.824 = -1422.224

P1i = xxxx i + yyyy j

P1i = 323.6868 = 323.6868 + 0 Veh1 in

P2i = -6111.766 = -7421.8 + -1310.034 Veh2 in

P1o = -6328.998 = -6434.262 + 105.264 Veh1 out

P2o = -2085.008 = -662.784 + -1422.224 Veh2 out

 

[gneill]

Okay let's try again.

weight 13158kg
heading 0 deg
departure 179
impact velocity 0.0246 m/s
departure velocity 0.49 m/s

weight 1726 kg
heading 190
departure 245
impact velocity 4.374 m/s
departure velocity 0.91 m/s

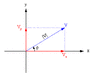
*V1ix = in V1ox = out


V1ix = 13158 * .0246 = 323.6868
V2ix = 1726 * -4.30 = -7421.8
V1ox = 1318 * -0.489 = -6434.262
V2ox = 1726 * -0.384 = -662.784


V1iy = .0246 * sin 0 = 0
V2iy = 1726 * -0.759 = -1310.034
V1oy = 13258 * 0.008 = 105.264
V2oy = 1726 * -0.824 = -1422.224

P1i = xxxx i + yyyy j

P1i = 323.6868 = 323.6868 + 0 Veh1 in

P2i = -6111.766 = -7421.8 + -1310.034 Veh2 in

P1o = -6328.998 = -6434.262 + 105.264 Veh1 out

P2o = -2085.008 = -662.784 + -1422.224 Veh2 out

I'm not sure what the values in red are meant to represent, but you've got the components of the vectors displayed which is good. The values are a little imprecise, perhaps due to not keeping enough significant figures in intermediate results (such as values of sin or cos)? Also, you should keep include the "i: and "j" in the notation to make sure that it is clear which component is which. That way in some future problem when you're dealing with THREE components and not just two, you can keep them straight when, say, the "j" component happens to be zero...

I figure the vectors should look like:

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

Note that I've kept three decimal places for these intermediate results. This will help prevent rounding errors from getting into the final results.

Now, in order to find the initial momentum vector you should add vectors p1i and p2i. That means summing their like components (add the x components, add the y components, and end up with Pi = xxxxxx i + yyyyyy j).

Do the same with the final momenta, adding p1o and p2o.

What do you get?

 

[Probie1]

I don't know why they came out in red, never mind them... I thought I was suppose to add them together that way.

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1i = 7758.517 i + 1310.961 j


p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

p2o = -7110.273 i + -1310.978 j

 

[gneill]

I don't know why they came out in red, never mind them... I thought I was suppose to add them together that way.

Actually, I added the red highlighting in the quote in order to draw attention to them

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1i = 7758.517 i + 1310.961 j


p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

p2o = -7110.273 i + -1310.978 j

Oops. mind the signs in the first addition. The second one looks good.

 

[Probie1]

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1i = -7111.143 i + 1310.961 j


p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

p2o = -7110.273 i + -1310.978 j

 

[gneill]

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1i = -7111.143 i + 1310.961 j


p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

p2o = -7110.273 i + -1310.978 j

There's still a sign issue with the j component of the initial momentum vector. When you add (0.000) to (-1310.961), what's the result?

When that's sorted, you will be in a position to directly compare the components of the initial momentum and final momentum vectors.

 

[Probie1]

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1i = -7111.143 i + -1310.961 j

p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

p2o = -7110.273 i + -1310.978 j

 

[gneill]

p1i = 323.687 i + 0.000 j
p2i = -7434.830 i - 1310.961 j

p1i = -7111.143 i + -1310.961 j

p1o = -6446.483 i + 112.523 j
p2o = -663.790 i - 1423.501 j

p2o = -7110.273 i + -1310.978 j

Much better.

So, now you can directly compare the components of the two momentum vectors, or if you wish, convert them to polar form (magnitude and angle) and compare them that way.

 

[Probie1]

That results are very close... probably be right on if I did not shorten my after decimal digits.
Thank you for all the patients you have shown me throught this... you should get a medal for all you do.

Now if I can copy this stuff down properly I will never forget how to do it on my own.

You are the BEST... thank you so much!

 

[gneill]

That results are very close... probably be right on if I did not shorten my after decimal digits.

Even using extended precision in the intermediate results, you can only expect the results to be as good as the initial data supplied in the problem. No doubt the angles and speeds given were rounded, too. So a couple of digits of accuracy is about all you can expect. In this case, it should be enough to see that momentum is being conserved, at least to the provided accuracy.

Thank you for all the patients you have shown me throught this... you should get a medal for all you do.

Now if I can copy this stuff down properly I will never forget how to do it on my own.

You are the BEST... thank you so much!

It's my pleasure to have been of help. Good luck in your studies!

 

[Probie1]

Yes... you are correct about the velocities and angles being rounded, and I will never again say that (P)i doesn't = (P)o.

Thanks a Million.