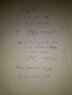Divya
- 9
- 1
- Homework Statement
- A rigid horizontal smooth rod $AB$ of mass $0.75 kg$ and length $40 cm$ can rotate freely about a fixed vertical axis through its mid point $O$. Two rings each of mass $1 Kg$ are initially at rest at a distance of $10 cm$ from $O$ on the either side of the rod.The rod is set in rotation with an angular velocity of $30$ radians per second. Find the velocity of each ring along the length of the rod in m/s when they reach the ends of the rod.
- Relevant Equations
- (I am new to this forum, I don't know what to write in 'Relevant Equations' field)
Method 1: Simply conserving angular momentum about the the fixed vertical axis and conserving energy gives ##v=3##, which is correct according to my book.
Method 2: Conserving angular momentum when the two rings reach distance ##x## from the centre gives
##(0.01+2x^2) \omega =0.9##
Also in the rod's frame ##a=v dv/dx =\omega ^2 x## (where a and v radial acceleration and velocities).
So, ##v^2/2=\int_{0.1}^{0.2} \frac {0.9xdx} {(0.01+2x^2)^2}=5##.
So, ##v=\sqrt{10}##.
What is wrong in second method?
Edit: Everything is in SI unit
Method 2: Conserving angular momentum when the two rings reach distance ##x## from the centre gives
##(0.01+2x^2) \omega =0.9##
Also in the rod's frame ##a=v dv/dx =\omega ^2 x## (where a and v radial acceleration and velocities).
So, ##v^2/2=\int_{0.1}^{0.2} \frac {0.9xdx} {(0.01+2x^2)^2}=5##.
So, ##v=\sqrt{10}##.
What is wrong in second method?
Edit: Everything is in SI unit
Last edited: