Why is the Voltmeter Showing 220V in a Broken Circuit?

[otomanb]

As every body knows in series voltage drops and voltmeter is applied in parallel but look at this image . as the circuit is broken and voltmeter is applied but still Vmeter is showing 220V?
how?

 

[gnurf]

The voltmeter has infinite internal resistance, so there is no current flowing in the circuit. What's the drop over the resistors? What did you expect?

 

[Dickfore]

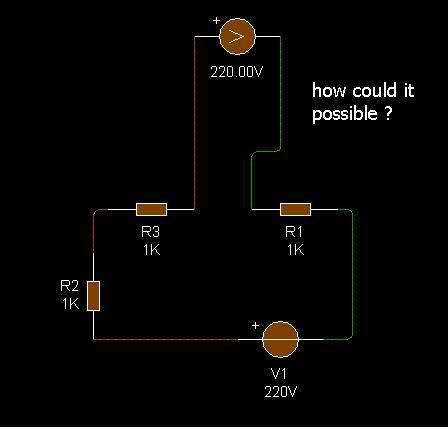
If the internal resistance of the voltmeter is r, then, the voltage drop across it is:

<br /> V = \frac{(220 \, \mathrm{V}) \, r}{1 \, \mathrm{k \Omega} + 1 \, \mathrm{k \Omega} + 1 \, \mathrm{k \Omega} + r}<br />

If the voltmeter is digital and the precision is 0.01 V, it means that everything above 219.995 V will be rounded up to 220 V, so:

<br /> \frac{(220 \, \mathrm{V}) \, r}{1 \, \mathrm{k \Omega} + 1 \, \mathrm{k \Omega} + 1 \, \mathrm{k \Omega} + r} &gt; 219.995 \, \mathrm{V}<br />
<br /> 220 \, r &gt; (3 \, \mathrm{k \Omega} + r) \, 219.995<br />
<br /> 0.005 \, r &gt; 659.985 \, \mathrm{k\Omega}<br />
<br /> r &gt; 1.32 \times 10^5 \, \mathrm{k\Omega} = 132 \, \mathrm{M\Omega}<br />

So, the internal resistance of the voltmeter is very high.

 

[otomanb]

actually this question was asked by our teacher in exams i answered 0 volts but when i checked it with a software livewire 1.11 it answers 220 V who is rite?

 

[gnurf]

The Machine is right, human.

 

[otomanb]

but the circuit is open so there is no current flowing
v=IR
I=0A so
v=0*any Resistance = 0volt
but software is saying 200.
it's contrary with the theories that we read before in book.
on thing more voltmeter is always applied in parallel with the load here in pic the voltmeter is not applied to parallel even though it's not parallel the resistors or voltage source.
please help!

 

[Dickfore]

but the circuit is open so there is no current flowing
v=IR
I=0A so
v=0*any Resistance = 0volt
but software is saying 200.
it's contrary with the theories that we read before in book.
on thing more voltmeter is always applied in parallel with the load here in pic the voltmeter is not applied to parallel even though it's not parallel the resistors or voltage source.
please help!

read my post.

 

[otomanb]

ohhhh! got that one!
you mean there is no current flowing so voltmeter is telling the source voltages 220. and there is no voltage drop?

got that one! thank you !

 

[Dickfore]

No, I meant the voltage drop on the remaining 3 resistors is smaller than 0.005 V and the voltmeter cannot register any difference with its sensitivity.

 

[otomanb]

thank you sir!

 

[Nevertamed]

it means the electrons are just 'waiting' for the continuity of the circuit be stablish in the ends of the 'break'