- #1
MagicPandaLol
- 8
- 1
Hey! I have a question and a drew up a diagram to help out. I drew up a circuit that includes just a voltage source and a resistor. I know the voltage is constant in each of the circled portions of the circuit. As in, as you move through the wiring, the voltage doesn't change from one point to the next. Really, the voltage only changes when you move through the load. This much I know, haha.
The source of my confusion is I don't know why this happens. If voltage is supposed to be the driving force that moves the current, how can the electrons move from one point to the next if the voltage isn't changing? After all, there isn't a difference in energy states from one point to the next within the wiring, so what's causing the motion?
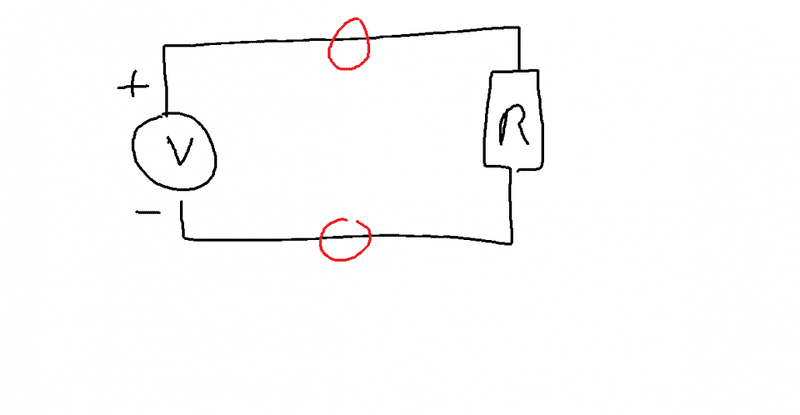
This has been what's bothering me. Any and all help is appreciated!
The source of my confusion is I don't know why this happens. If voltage is supposed to be the driving force that moves the current, how can the electrons move from one point to the next if the voltage isn't changing? After all, there isn't a difference in energy states from one point to the next within the wiring, so what's causing the motion?
This has been what's bothering me. Any and all help is appreciated!