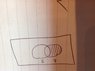
Why P(A|B') not P(A)-P(A n B)?

  • Context: Undergrad 
  • Thread starter Thread starter CAH
  • Start date Start date
Click For Summary
SUMMARY

The discussion clarifies the distinction between conditional probability P(A|B') and the expression P(A) - P(A ∩ B). It establishes that P(A|B') = P(A ∩ B) / P(B') is valid only when B' is considered, excluding events in A ∩ B from the sample space. The participants emphasize that the probability space for P(A|B') does not include events from A ∩ B, which is crucial for accurate probability calculations. Misinterpretation arises when applying Venn diagrams without recognizing the different probability spaces involved.

PREREQUISITES
  • Understanding of basic probability concepts, including conditional probability.
  • Familiarity with probability spaces and their implications.
  • Knowledge of set theory, particularly intersections and complements.
  • Ability to interpret Venn diagrams in the context of probability.
NEXT STEPS
  • Study the concept of probability spaces in detail.
  • Learn about conditional probability and its applications in real-world scenarios.
  • Explore the implications of Venn diagrams in probability theory.
  • Investigate advanced topics in probability, such as Bayesian inference.
USEFUL FOR

Students of probability theory, mathematicians, statisticians, and anyone seeking to deepen their understanding of conditional probability and its applications.

CAH
Messages
48
Reaction score
0
I know the equations that P(A|B') = P(AnB) / P(B')

But why isn't it P(A) - P(A n B)

See photo attachment

We know b didn't happen so isn't it just A minus the middle?
 

Attachments

  • image.jpg
    image.jpg
    40 KB · Views: 465
Physics news on Phys.org
P(A)=P(A ∩ B )+P(A ∩ B')
P(A|B')=P(A ∩ B')/P(B')

Your version will hold only of P(B')=1.
 
Specifically, P(A | B^{C}) := P(A) - P(A \cap B) would still include B in the sample space. Given that B hasn't happen, you don't want B in the sample space.
 
CAH said:
I know the equations that P(A|B') = P(AnB) / P(B')

But why isn't it P(A) - P(A n B)

In an expression for probability P(S), there are more things involved that the set S. The expression for a probability involves (perhaps implicitly) a particular "probability space". The expressions P(A|B') and P(A \cap B') both refer to the same set. However, they refer to different probability spaces. In the probability space for P(A|B') no events in A \cap B exist. In the probability space for A \cap B' , events in A \cap B may exist and may be assigned nonzero probabilities.

Your reasoning with the Venn diagram doesn't include the information about what sets are in the two different probability spaces.
 

Similar threads

Undergrad Can you calculate the probability of a complex logic expression?
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Understanding extinction probability in simple GWP
  • · Replies 1 ·
Replies
1
Views
2K
Undergrad Ways to put n balls in m boxes such that exactly k boxes are empty?
  • · Replies 29 ·
Replies
29
Views
4K
High School Relative And Absolute Probability (Probability Of Picking A Red Ball)
  • · Replies 8 ·
Replies
8
Views
3K
Undergrad Prove that the tail of this distribution goes to zero
  • · Replies 2 ·
Replies
2
Views
2K
Graduate Chernoff Bounds using importance sampling identity
  • · Replies 0 ·
Replies
0
Views
2K
Undergrad Martingale, Optional sampling theorem
  • · Replies 6 ·
Replies
6
Views
2K
Undergrad Translate compound proposition p → q (implication) to p↓q question
  • · Replies 4 ·
Replies
4
Views
2K
High School How to calculate this conditional probability?
  • · Replies 7 ·
Replies
7
Views
864
Undergrad Write probability in terms of shape parameters of beta distribution
  • · Replies 1 ·
Replies
1
Views
2K