Wiki on e (mathematical constant)

[Pellefant]

The source: http://en.wikipedia.org/wiki/E_(mathematical_constant)

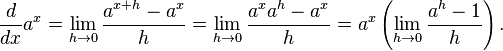
I can not understand the last peace in that equation,

If e=a it will be e^x*((1-1)/0) ...which means 0/0, that don't make sense :(, what am i missing

 

[neutrino]

Write e^h as an infinite series.

 

[HallsofIvy]

What you are quoting from Wikipedia is the "difference quotient" calculation for the deriviative of a^x:
$$\frac{d}{dx}a^x= \lim_{h\rightarrow 0}\frac{a^{x+h}-a^x}{h}= \lim_{h\rightarrow 0}\frac{a^xe^h-a^x}{h}= a^x \lim_{h\rightarrow 0}\frac{a^h- 1}{h}$$

Now, I'm not at all sure what you mean by "If e=a it will be e^x*((1-1)/0) ...which means 0/0". Whether e= a or not, if you replace h by 0 in the limit, you get (1-1)/0 which does not exist. But that's not how you find limits! What you can do is show that
$$\lim_{h\rightarrow 0} \frac{a^h- 1}{h}$$
does, in fact, exist so that the derivative of a^x exists and is just that constant times a^x. You can then define e to be the value of a such that that limit is 1, giving $d e^x/dx= e^x$.

 

[robert Ihnot]

When you are looking at a limit process, you can see how numbers work. For example

F(n) = (1+1/n)^n, give us values F(1) = 2, F(2)=2.25; F(5) = 2.49, F(10) = 2.59; F(100) = 2.70, and as we approach infinity it goes to e=2.71828...