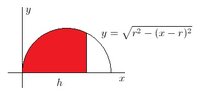
First, we may find the volume of the submerged portion of the ball by rotating the following shaded area about the $x$-axis using the disk method:
View attachment 1224
The volume of an arbitrary disk is:
$$dV=\pi R^2\,dx$$
where:
$$R^2=y^2=r^2-(x-r)^2=2rx-x^2$$
And so we have:
$$dV=\pi\left(2rx-x^2 \right)\,dx$$
Summing the disks through integration, we obtain:
$$V=\pi\int_0^h 2rx-x^2\,dx=\pi\left[rx^2-\frac{x^3}{3} \right]_0^h=\frac{\pi h^2}{3}(3r-h)$$
This is the volume of the so-called "spherical cap."
Next, using the principle of Archimedes, we may equate the mass of the sphere to the mass of the fluid it displaces. Let $\rho$ be the mass density of the fluid, and $k\rho$ be the mass density of the sphere, where $0<k<1$. Mass density is mass per volume, and so mass is mass density times volume, hence, we may write:
$$k\rho\left(\frac{4}{3}\pi r^3 \right)=\rho\left(\frac{\pi h^2}{3}(3r-h) \right)$$
Simplifying, we obtain:
$$4k=\left(\frac{h}{r} \right)^2\left(3-\frac{h}{r} \right)$$
Let $$u=\frac{h}{r}$$, and we may write:
$$u^3-3u^2+4k=0$$
We are told $$k=\frac{4}{5}$$ and so we have:
$$u^3-3u^2+4\left(\frac{4}{5} \right)=0$$
And multiplying through by 5, we obtain:
$$5u^3-15u^2+16=0$$
As we are allowed to obtain a numerical solution, we need not work with the rather cumbersome cubic formula.
Because $$\frac{1}{2}<k<1$$, it is reasonable to assume $1<u<2$, so a good first estimate is $$u=\frac{3}{2}$$. Using Newton's method, where:
$$f(u)=5u^3-15u^2+16=0$$
$$f'(u)=15u^2-30u$$
we obtain the recursion:
$$u_{n+1}=u_n-\frac{5u_n^3-15u_n^2+16}{15u_n^2-30u_n}=\frac{u_n\left(15u_n^2-30u_n \right)-\left(5u_n^3-15u_n^2+16 \right)}{15u_n\left(u_n-2 \right)}=\frac{10u_n^3-15u_n^2-16}{15u_n\left(u_n-2 \right)}$$
Thus, we may compute:
$$u_0=1.5$$
$$u_1=1.4\overline{2}$$
$$u_2\approx1.42571225071225$$
$$u_3\approx1.42571854914589$$
$$u_4\approx1.42571854916652$$
$$u_5\approx1.42571854916652$$
And so we find:
$$h\approx1.42571854916652r$$