Word problem involving algebra/angles

[Arringar]

The Sun, at a distance of 149.6 million km from Earth, subtends about the same angle in the sky as does the Moon, with a radius of 1737 km at a distance of 384,400 km from Earth. Use this information to find the radius of the Sun in km. Round your answer to three significant figures.

Can someone show me (in detail) how to solve this, please? I want to understand the concepts thoroughly so the more detailed the explanation the better.

 

[soroban]

Hello, Arringar!

Did you make a sketch?

The Sun, at a distance of 149.6 million km from Earth,
subtends about the same angle in the sky as does the Moon,
with a radius of 1737 km at a distance of 384,400 km from Earth.
Use this information to find the radius of the Sun in km.
Round your answer to three significant figures.

                                          * S
                                    *     |
      :- 384,400 -:           *           |
                  M     *                 |
                  *                       |
            *     |O                      |
    E * - - - - - * - - - - - - - - - - - * U
            *     | 1737                  |
                  *                       |
                  N     *                 | r
                              *           |
                                    *     |
                                          * N
      : - - - - -  149,600,000  - - - - - :

The Earth is at E.

The Moon's diameter is MN; its radius is ON = 1737 km.
Its distance is EO = 384,\!400 km.

The Sun's diameter is SN; its radius is UN = r km.
Its distance is EU = 149,\!600,\!000 km.

From similar triangles, we have: .\frac{r}{1737} \:=\:\frac{149,\!600,\!000}{384,\!400}

Solve for r.

 

[MarkFL]

I am certain the method soroban has posted (or something similar) is what you are expected to use, but...let's see if we can make it a bit more complicated.(Tmi)

Normally, distances between celestial bodies is center-to-center. Let's assume our observer is on the line which connects the centers of the the Earth and the other bodies.

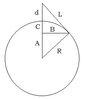
For the calculations to follow, please refer to this diagram:

View attachment 497

$\displaystyle d$ is the distance from the observer to the surface of the other body, either the Moon or the Sun.

$\displaystyle L$ is the distance to the horizon, or line of sight. $\displaystyle A+C=R$.

By similarity, we have:

$\displaystyle \frac{L}{C+d}=\frac{R+d}{L}$

We want to find $\displaystyle C$ in terms of $\displaystyle R$ and $\displaystyle d$:

$\displaystyle \frac{L}{C+d}=\frac{R+d}{L}$

$\displaystyle L^2=(C+d)(R+d)=CR+Cd+dR+d^2$

By Pythagoras, we also have:

$\displaystyle L^2=(R+d)^2-R^2=2dR+d^2$ thus:

$\displaystyle CR+Cd+dR+d^2=2dR+d^2$

$\displaystyle C(R+d)=dR$

$\displaystyle C=\frac{dR}{R+d}$

$\displaystyle L=\sqrt{d(2R+d)}$

Now, if we subscript measures pertaining to the Moon with $\displaystyle M$ and those pertaining to the Sun with $\displaystyle S$, we have by similarity:

$\displaystyle \frac{L_S}{C_S+d_S}=\frac{L_M}{C_M+d_M}$

$\displaystyle \frac{\sqrt{d_S(2R_S+d_S)}}{\frac{d_SR_S}{R_S+d_S}+d_S}=\frac{\sqrt{d_M(2R_M+d_M)}}{\frac{d_MR_M}{R_M+d_M}+d_M}$

$\displaystyle \frac{(R_S+d_S)\sqrt{d_S(2R_S+d_S)}}{d_S(2R_S+d_S)}=\frac{(R_M+d_M)\sqrt{d_M(2R_M+d_M)}}{d_M(2R_M+d_M)}$

$\displaystyle \frac{R_S+d_S}{\sqrt{d_S(2R_S+d_S)}}=\frac{R_M+d_M}{\sqrt{d_M(2R_M+d_M)}}$

$\displaystyle (R_S+d_S)\sqrt{d_M(2R_M+d_M)}=(R_M+d_M)\sqrt{d_S(2R_S+d_S)}$

$\displaystyle (R_S+d_S)^2d_M(2R_M+d_M)=(R_M+d_M)^2d_S(2R_S+d_S)$

$\displaystyle d_S(R_S+(R_S+d_S))=\frac{(R_S+d_S)^2d_M(2R_M+d_M)}{(R_M+d_M)^2}$

Now, if we observe that (where the radius of the Earth is $\displaystyle R_E$):

$\displaystyle R_S+d_S=r_S-R_E$

$\displaystyle R_M+d_M=r_M-R_E$

where:

$\displaystyle r_S$ is the center-to center distance from the Earth to the Sun,

$\displaystyle r_M$ is the center-to center distance from the Earth to the Moon,

then we have:

$\displaystyle ((r_S-R_E)-R_S)(R_S+(r_S-R_E))=\frac{(r_S-R_E)^2(r_M-(R_E+R_M))(R_M+r_M-R_E)}{(r_M-R_E)^2}$

$\displaystyle (R_S+(r_S-R_E))(R_S-(r_S-R_E))=\frac{(r_S-R_E)^2((R_E+R_M)-r_M)(R_M+r_M-R_E)}{(r_M-R_E)^2}$

$\displaystyle R_S^2-(r_S-R_E)^2=\frac{(r_S-R_E)^2((R_E+R_M)-r_M)(R_M+r_M-R_E)}{(r_M-R_E)^2}$

$\displaystyle R_S^2=\frac{(r_S-R_E)^2((R_E+R_M)-r_M)(R_M+r_M-R_E)}{(r_M-R_E)^2}+(r_S-R_E)^2$

$\displaystyle R_S^2=\frac{(r_S-R_E)^2\left(((R_E+R_M)-r_M)(R_M+r_M-R_E)+(r_M-R_E)^2 \right)}{(r_M-R_E)^2}$

$\displaystyle R_S^2=\frac{(r_S-R_E)^2\left((R_M-(r_M-R_E))(R_M+(r_M-R_E))+(r_M-R_E)^2 \right)}{(r_M-R_E)^2}$

$\displaystyle R_S^2=\left(\frac{R_M(r_S-R_E)}{(r_M-R_E)} \right)^2$

Taking the positive root, we have:

$\displaystyle R_S=\frac{R_M(r_S-R_E)}{r_M-R_E}$

All that, only to find that since the Sun and Moon subtend the same angle, the observer is seeing the same portion of the surface, which can be shown using calculus to be given by:

$\displaystyle \frac{d}{2(R+d)}$

I thought we were to essentially make the assumption that we were viewing half of the surfaces of the Sun and the Moon, i.e., using:

$\displaystyle \lim_{d\to\infty}\frac{d}{2(R+d)}=\frac{1}{2}$

so that we could use similarity, but in fact, similarity is preserved without this assumption. From the very beginning then, we could have simply stated:

$\displaystyle \frac{R_S}{R_M}=\frac{r_S-R_E}{r_M-R_E}$

and avoided the vast majority of the algebra above.(Smirk)

So, using $\displaystyle R_E=6378.1\text{ km}$ and the other given values, we find (to 3 decimal places):

$\displaystyle R_S\approx6.87\times10^5\text{ km}$

 

[CaptainBlack]

I am certain the method soroban has posted (or something similar) is what you are expected to use, but...let's see if we can make it a bit more complicated.(Tmi)

Normally, distances between celestial bodies is center-to-center. Let's assume our observer is on the line which connects the centers of the the Earth and the other bodies.

For the calculations to follow, please refer to this diagram:

https://www.physicsforums.com/attachments/497

<...snip...>

so that we could use similarity, but in fact, similarity is preserved without this assumption. From the very beginning then, we could have simply stated:

$\displaystyle \frac{R_S}{R_M}=\frac{r_S-R_E}{r_M-R_E}$

and avoided the vast majority of the algebra above.(Smirk)

So, using $\displaystyle R_E=6378.1\text{ km}$ and the other given values, we find (to 3 decimal places):

$\displaystyle R_S\approx6.87\times10^5\text{ km}$

There is an implicit assumption here that the Sun and Moon subtend the same angle when they are at the zenith, but you can experience the Sun rising totally eclipsed, when to all intents and purposes you could ignore the size of the Earth.

In fact with the right configuration the Moon subtends a smaller angle that the Sun and you can get an annular eclipse. (Typically the Moon subtends a greater angle that the Sun by ~0.5 minutes of arc but has a greater variation that the Sun (~2.5 as opposed to ~0.5 minutes of arc)

Further info: the Sun and Moon both subtend about 1/2 a degree (30 minutes of arc ~9 milli-radian, which is about the same angle a 5mm at arms length - yes I just measured my arms length to check that)

CB