Wording question regards angles

[Benn]

I have two angles:

θ:

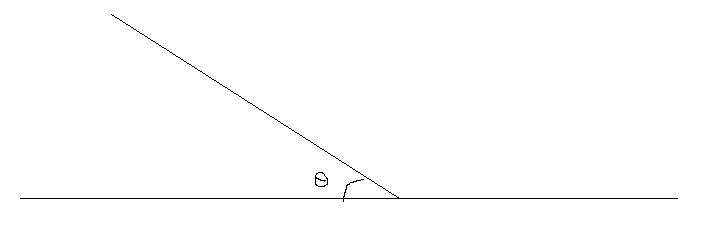
and θ_{1}:

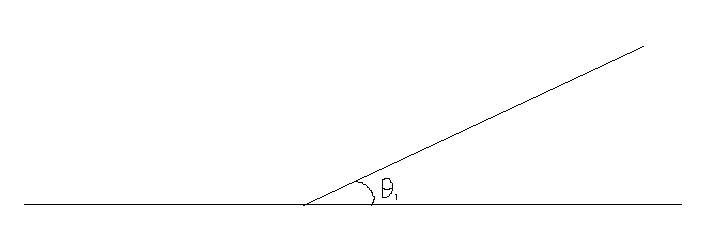
θ_{1} = θ

How do I differentiate the two angles? I want to say "leftward facing" and "rightward facing", but I'm not sure how to "mathematically." Note that I must talk about the angle that's between 0-90 degrees.

Thanks,
Ben

 

[chiro]

Hey Benn and welcome to the forums.

In terms of an 'angle' as a quantity, we don't differentiate them in the way that you have described.

However what is done in geometry is that we can reference an angle in terms of three points. The three points denote a triangle where the order of the point denotes the angle and its orientation. For example if we denote ABC as an angle then given points A, B, and C the angle is formed by looking at the interior of the triangle ABC where the angle is between the points A and C.

The idea can be applied to higher levels of geometry where orientation comes in, but for your kind of geometry that you are describing, it probably might be better if you use the above convention.

If you are interested in orientation in high level geometry, then you need to understand the determinant and the wedge product. It would help you to understand three-dimensional vector algebra which includes the cross-product which helps identify methods to incorporate orientation (your left facing and right facing angles) in a way that one orientation produces one vector and the reverse orientation produces a vector that is opposite to that vector.

If you are going to do the above, you have to treat your lines as vectors and speak about things in that context.

Have you ever learned about vectors or vectors and geometry before? What mathematical background do you have?

 

[gsal]

If in your context, your angles are going to be in specific places, maybe you want to refer to one of them as being in the first quadrant and the other one in the second...maybe?