Work and changing forces - Integration

[urbanyoung]

Hi,

I'm doing some mechanics study and one thing keeps confusing me. In the textbook (Serway/Jewett Physics for scientists and engineers, 7th ed) they introduce i into integral equations. I've put a picture of it below to save me from trying to type the symbols. The equation is for the work done by a spring.

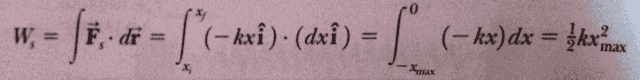
I'm hoping someone can explain to me what is being done. I thought it would be dot product, but doesn't that introduce a cosine of the angle? I'm also not sure what the dr is, or well, what the r is.

Thanks.

 

[jtbell]

In this case, i is a unit vector (vector with magnitude 1) that points in the +x direction. i dot i = (1)(1)cos(0) = 1. In this case, the book apparently assumes that both the force and the displacement are along the x-axis.

 

[SteamKing]

The equation for work indeed involves the dot product. The integral used to calculate work does so by analyzing the vector force F and the path of its application. The path is split into tiny elements dr. For the particular application, namely compressing a spring, the force is acting along the x-axis, which is why dr changes to dxi. Similarly, the force compressing the spring is a function of the spring constant k and the amount the spring is compressed, xi. Remember, when a vector is dotted with itself, like i*i is in the integral, the resulting scalar quantity is the square of the length of the original vector, which is 1 for i. Since the angle between a vector and itself is zero, the cosine is equal to 1.

 

[Studiot]

The equation is for the work done by a spring.

Since this is a spring its a pretty fair assumption that only one axis need be considered.
You would have to go into 3D for the general case.

 

[PJC01]

Hello,

I can understand how this equation may be confusing at first. The i in the integral equation is actually representing a unit vector in the x-direction. This is because the work done by the spring is only in the x-direction, so we are only considering the displacement in that direction. The dr represents a small displacement in the x-direction, which is why it is written as dx. The r in this case is the position vector, which is typically written as r = xi + yj + zk in three dimensions, but since we are only considering the x-direction in this equation, it is written as just r = xi.

As for the cosine, it is actually taken into account by the dot product. The dot product of two vectors gives us the component of one vector in the direction of the other vector, which is why we use it in this equation. So, while the cosine is not explicitly written, it is accounted for in the dot product.

I hope this explanation helps clarify things for you. Keep up the good work with your mechanics studies!