x86
Gold Member
- 256
- 18
This is a concept that has long since plagued me. I will quote an article off of Google about the concept I am confused about:
"Consider a collection of
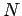 static point charges
static point charges
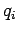 located at position vectors
located at position vectors
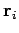 (where
(where
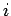 runs from 1 to
runs from 1 to
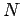 ). What is the electrostatic energy stored in such a collection? Another way of asking this is, how much work would we have to do in order to assemble the charges, starting from an initial state in which they are all at rest and very widely separated? " [http://farside.ph.utexas.edu/teaching/em/lectures/node56.html]
). What is the electrostatic energy stored in such a collection? Another way of asking this is, how much work would we have to do in order to assemble the charges, starting from an initial state in which they are all at rest and very widely separated? " [http://farside.ph.utexas.edu/teaching/em/lectures/node56.html]
So, I understand the general concept. But I am confused in one of the cases. The case where the work that we do is negative (i.e. the work that we have to do to assemble the charge is < 0).
Here is an example that I will use to illustrate my confusion:
Say that we have two charges q in space, one positive, and one negative, and want to move them close to each other, to a distance of r.
The answerof course, is that the work that we need to do to bring the negative charge to the positive charge is then W = -kq^2/r < 0. I know this is the answer, and I know how to solve these problems. But I have no idea why this is true.
I am confused about the concept. I will try to explain what I am confused about below:
It is known that W = Fd. In this case , d = (infinity - r)
But I am confused about this, because essentially the charges attract one another. Therefore, we don't really have to apply any force to make them get close to each other, because an electric force will handle this for us. So our applied force F = 0. Then W = 0*d = 0. But of course, this is wrong. Because we know the answer to be W = -kq^2/r. But why?
"Consider a collection of
So, I understand the general concept. But I am confused in one of the cases. The case where the work that we do is negative (i.e. the work that we have to do to assemble the charge is < 0).
Here is an example that I will use to illustrate my confusion:
Say that we have two charges q in space, one positive, and one negative, and want to move them close to each other, to a distance of r.
The answerof course, is that the work that we need to do to bring the negative charge to the positive charge is then W = -kq^2/r < 0. I know this is the answer, and I know how to solve these problems. But I have no idea why this is true.
I am confused about the concept. I will try to explain what I am confused about below:
It is known that W = Fd. In this case , d = (infinity - r)
But I am confused about this, because essentially the charges attract one another. Therefore, we don't really have to apply any force to make them get close to each other, because an electric force will handle this for us. So our applied force F = 0. Then W = 0*d = 0. But of course, this is wrong. Because we know the answer to be W = -kq^2/r. But why?
Last edited by a moderator: