Work Done by a General Variable Force

[musicfairy]

A 8 kg brick moves along an x axis. Its acceleration as a function of its position is shown in Figure 7-37. What is the net work performed on the brick by the force causing the acceleration as the brick moves from x = 0 to x = 8.0 m?

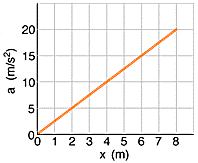
What I tried to do is find the area and multiply by the mass, but it doesn't work.

Please help.


Edit: Never mind it worked. I just typed it in wrong. But I have another concern.

Is there any additional ways to solve this problem other than the one I mentioned? I was looking at someone else's work and that person did something with the slope. How does that work?

 

[Rake-MC]

By looking at it I could see that if they take info from the slope they would appear to be taking a longer route, finding the slope just cancels the displacements.

 

[baba89]

There are several ways to solve this problem, and the method you described (finding the area under the curve and multiplying by mass) is one valid approach. Another method is to use the equation W = Fd, where W is the work done, F is the force, and d is the distance. In this case, the force is varying with position, so you would need to integrate the force function to find the total work done.

As for the method involving slope, it is likely that the person used the concept of work-energy theorem, which states that the net work done on an object is equal to the change in its kinetic energy. By finding the slope of the acceleration vs. position graph, they may have been able to calculate the change in kinetic energy and thus the net work done. However, this method may not work for all cases and may require additional assumptions or equations. It is always important to carefully consider the method and assumptions used in solving a physics problem.