Work done by a tangential force

[Zang]

Homework Statement

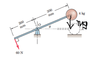
The 4-kg ball and the attached light rod rotate in the vertical plane about the fixed axis at O. If the assembly is released from rest at and moves under the action of the 60-N force, which is maintained normal to the rod, determine the velocity v of the ball as approaches . Treat the ball as a particle.

Homework Equations

T₂ = U_1-2 + T₁
s = rθ
T = 0.5mv²

3. The Attempt at a Solution
200mm = 0.2m; 300mm = 0.3m
s = 0.2(π/2) = 0.1π
T₁ = 0
T₂ = U_1-2 = 60(0.1π) + mg(0.3) = 30.622J
v = ((2*30.622)/4)^0.5 = 3.91 m/s but my answer is wrong

 

[scottdave]

I am not following your symbology. But it looks like you took the work done (force tangent to circular arc, multiplied by distance traveled), then you add that to the increase in gravitational potential energy and equate that to the kinetic energy?

What is the net energy input? What is the change in system energy? Those two must equal each other.

 

[Zang]

I am not following your symbology. But it looks like you took the work done (force tangent to circular arc, multiplied by distance traveled), then you add that to the increase in gravitational potential energy and equate that to the kinetic energy?

What is the energy input? What is the change in system energy? Those two must equal each other.

In my textbook, U is work and T is kinetic energy. I just figured out I was supposed to subtract the work done by gravity, not add.