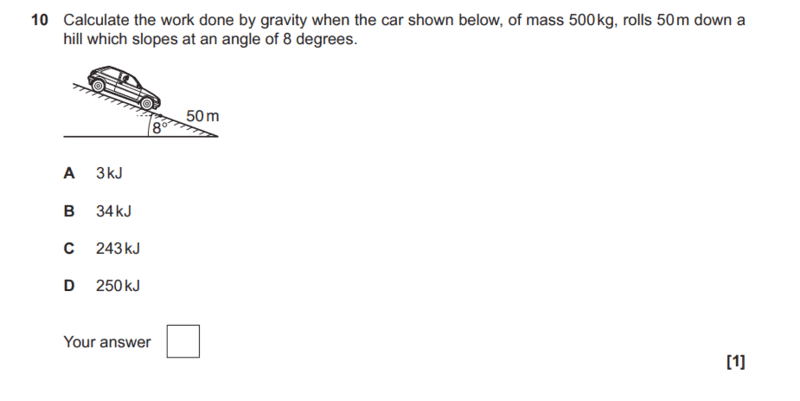Work done by gravity on a car rolling down a hill

Click For Summary
SUMMARY

The discussion focuses on calculating the work done by gravity on a car rolling down a hill using the formula W = ΔE_P instead of W = Fd cos θ. A participant initially attempted to use E = F x cos θ, resulting in an energy value of 243 kJ. The conversation highlights the importance of understanding the angle θ in the context of gravitational potential energy and suggests that the distance in the diagram is represented as 50 cos(8°) m.

PREREQUISITES
  • Understanding of gravitational potential energy (ΔE_P)
  • Familiarity with the work-energy principle
  • Knowledge of trigonometric functions, specifically cosine
  • Basic physics concepts related to forces and motion
NEXT STEPS
  • Study the work-energy theorem in classical mechanics
  • Learn about gravitational potential energy calculations
  • Explore trigonometric applications in physics problems
  • Review the implications of angle θ in work calculations
USEFUL FOR

Students studying physics, educators teaching mechanics, and anyone interested in understanding the principles of work and energy in gravitational contexts.

physicsmaster123
Messages
3
Reaction score
0
Thread moved from the technical forums to the schoolwork forums
I tried E =Fxcos0 but only ended up with 243kJ
1694284850662.png
 
Last edited by a moderator:
Physics news on Phys.org
What values of ##F##, ##x##, and ##\theta## did you use and why?
 
Reply
  • Like
Likes   Reactions: Lnewqban
Hint: What is the textbook definition of ##\theta## in the formula you stated?
 
Last edited:
physicsmaster123 said:
I tried E =Fxcos0 but only ended up with 243kJ
What distance in the diagram is ##50\cos(8°)##m?
 
Specific to this exercise, ##W=\Delta E_P## is a better fit than ##W=Fd\cos \theta##
 
Reply
  • Like
Likes   Reactions: Lnewqban

Similar threads

Combined Rotation and Translation of a Rectangular Plate
  • · Replies 9 ·
Replies
9
Views
2K
A block dropping onto a spring system
  • · Replies 58 ·
2
Replies
58
Views
3K
Kinetic Energy of a Cylinder Rolling Without Slipping
  • · Replies 21 ·
Replies
21
Views
5K
Final velocity of a car rolling down a ramp using energy
  • · Replies 1 ·
Replies
1
Views
3K
Why Does a Car Accelerate When Rolling Down a Hill?
  • · Replies 11 ·
Replies
11
Views
3K
Forces involved in principle of virtual work
  • · Replies 2 ·
Replies
2
Views
847
Why is the direction of kinetic/static friction up a ramp?
  • · Replies 7 ·
Replies
7
Views
1K
A cylinder of snow rolls down a hill gathering more snow -- calculate its speed
  • · Replies 39 ·
2
Replies
39
Views
3K
Work & Energy (Question on Classical Mechanics/Slope based Problems)
  • · Replies 7 ·
Replies
7
Views
2K
Thermodynamic Work vs Mechanical Work
  • · Replies 3 ·
Replies
3
Views
1K