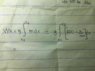Work done on an object given a variable mass

[Eucliwood]

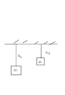
I was just doing some review on my physics lecture and I stumble on the idea of what if there was an object hanging and the cord mass is also included in the weight and it's displaced upward without having velocity nor time hypothetically and the cord change mass. I tried solving it by W = fΔx that I came up with this equation W = m1g(height initial - height final) - m2g(height initial - height final), but I'm certain integral is a must on this problem, but I don't know how to derive my own equation that the mass is dependent of the distance. I was wondering if any of you can give me any insight on how to solve this problem.

 

[Filip Larsen]

You have to make some assumption on how the mass increases as the block is lifted. Since the additional mass comes from a cord there is very natural assumption you can make about how the mass of the cord is distributed along its height. The idea is that you write up the total mass as a function of height, $m(h)$, that involves the two masses $m_1$ and $m_2$ and the given height $h$ (that varies between $h_1$ and $h_2$). If you are still stuck perhaps it will help plotting mass as a function of height on paper and putting in the values you know (symbolically) since you know that $m(h_1) = m_1$ and $m(h_2) = m_2$.

Then when you have an expression for mass as function of height you can write up the corresponding force of gravity on the block plus lifted cord as a function of height (assuming for instance, as you already have, that acceleration of gravity is constant in the interval $[h_1, h_2]$) and finally, as you correctly say, you can start write up the work integral itself.

 

[Eucliwood]

So, say a 2N/1m will be part of the equation of mass(h)? and since the integral is with respect to displacement i can integrate it?

 

[Filip Larsen]

So, say a 2N/1m will be part of the equation of mass(h)? and since the integral is with respect to displacement i can integrate it?

That is correct.

Usually one would like to use symbols as long as possible and only insert the actual numbers in the final result if possible, which it is here. For instance, the mass function can be expressed as $$m(x) = m_1 + \frac{m_2 - m_1}{x_2 - x_1}(x - x_1) = m_1 + k (x-x_1),$$ where $k = (m_2-m_1)/(x_2-x_1)$ is a constant (when integrating) expressing the cord mass per length.

Edit: formatting the LaTeX better.

 

[Eucliwood]

That is correct.

Usually one would like to use symbols as long as possible and only insert the actual numbers in the final result if possible, which it is here. For instance, the mass function can be expressed as $$m(x) = m_1 + \frac{m_2 - m_1}{x_2 - x_1}(x - x_1) = m_1 + k (x-x_1),$$ where $k = (m_2-m_1)/(x_2-x_1)$ is a constant (when integrating) expressing the cord mass per length.

Edit: formatting the LaTeX better.

Thank you! I've one last question, on the x is that the the Δx?

 

[Filip Larsen]

Thank you! I've one last question, on the x is that the the Δx?

I am not sure what you mean exactly?

The expression I wrote is mass as a function of the position $x$ that for this problem is defined from $x_1$ to $x_2$, so you can say that $\Delta x = x_2 - x_1$. I chose to name them $x_1$ and $x_2$ so the indices match those of $m_1$ and $m_2$. These are the same positions as what you have labelled $x_i$ and $x_f$ in your hand-written note, so another way to get consistency is to name the masses $m_i$ and $m_f$.

As you may have noticed, $x$ above is only used relative to $x_1$ so the absolute value of $x$ is not really needed. This means we can add or subtract any arbitrary constant we like from all positions and still get same result. Often this means we can choose one of the reference points to be labelled as zero and get a simpler expression where we don't have to carry around all those subtractions. For this problem we could for instance simplify by choosing $x_1 = 0$ and $x_2 = \Delta x = c$ for the positions and $m_1 = m$ and $m_2 = m + \Delta m = m + m_c$ for the masses to get $$m(x) = m + \frac{m_c}{c} x,$$ and then integrate from $0$ to $c$. It gives exact same result in the end but with fewer symbols to keep track of during calculations.