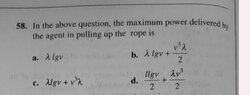erobz
Gold Member
- 4,459
- 1,846
To me it seems like to be consistent we always should be writing the following:
$$ W = \int F ~dx = \int \left( m \frac{dv}{dt} + v \frac{dm}{dt} \right) dx $$
Then we can see that for the chain at constant velocity ##v## problem:
$$ W = \int F ~dx = \int \left( \cancel{ m \frac{dv}{dt}} + v \frac{dm}{dt} \right) dx $$
$$ \implies \int F ~dx = \int v \frac{dm}{dt} dx = \int v \frac{dm}{dx} \frac{dx}{dt} dx = \int v \frac{dm}{dx} v dx = v^2 \int_{0}^{l} \lambda ~dx = \lambda l v^2 $$
However, that doesn't really play nicely either. That factor of ##\frac{1}{2}## out front is missing, or should it not actually be there?
$$ W = \int F ~dx = \int \left( m \frac{dv}{dt} + v \frac{dm}{dt} \right) dx $$
Then we can see that for the chain at constant velocity ##v## problem:
$$ W = \int F ~dx = \int \left( \cancel{ m \frac{dv}{dt}} + v \frac{dm}{dt} \right) dx $$
$$ \implies \int F ~dx = \int v \frac{dm}{dt} dx = \int v \frac{dm}{dx} \frac{dx}{dt} dx = \int v \frac{dm}{dx} v dx = v^2 \int_{0}^{l} \lambda ~dx = \lambda l v^2 $$
However, that doesn't really play nicely either. That factor of ##\frac{1}{2}## out front is missing, or should it not actually be there?