Northbysouth
- 241
- 2
Homework Statement
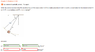
Write the vector expression for the acceleration a of the mass center G of the simple pendulum in both n-t and x-y coordinates for the instant when θ = 66° if θ'= 2.22 rad/sec and θ"= 4.475 rad/sec2
I have attached an image of the question.
Homework Equations
an = v2/r = rθ2 = vθ'
at = v' = rθ'
The Attempt at a Solution
I've managed to calculate en and et correctly
at = (4.2 ft)(4.475 rad/sec2) = 18.795 ft/sec2
at = 18.795ft/sec2
For an I calculated velocity first:
v = rθ' = (4.2ft)(2.22 rad/sec)
v = 9.324 ft/sec
Hence an = (9.324 ft/sec)(2.22 rad/sec)
an = 20.69928 ft/sec2
Unfortunately, I'm now having difficulty with finding the velocity in terms of i and j.
I had thought that I could use geometry to do it:
atcos(90-66) = -17.77 i
atsin(90-66) = 7.644 j
But the system says it's wrong. Help is greatly appreciated.