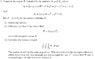- #1
Gameowner
- 45
- 0
Homework Statement
Question B)
Homework Equations
The Attempt at a Solution
So I know the flux of S1 U S2 is the same as the flux for S1 + flux of S2, that is
Double Int of S(surface) = Double Int of S1 U S2 = Double Int S1 + Double Int S2
The problem I'm having is parameterizing S1. I know for a cone(x^2+y^2=z^2) has the parametrization of x=rcos(theta), y=rsin(theta), z=z, and substituting it into the equation of a cone gives z=r, which means when you map it from one coordinate system into another it maps exactly one-to-one.
But If I were to use the same parametrization for my particular problem, that is, rearranging my equation of S1 so that I get z=f(x,y), and substituting in the parameterization(x=rcos(theta), y=rsin(theta)) then evaluating it, I get z=-3/4*r.
So I'm just wondering what I do from here? any hints and tips would be much appreciated.