- #1
tracyellen
- 14
- 0
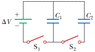
Consider the circuit shown in the figure below, where C1 = 4.00 µF, C2 = 7.00 µF, and ΔV = 18.0 V. Capacitor C1 is first charged by closing switch S1. Switch S1 is then opened, and the charged capacitor is connected to the uncharged capacitor by closing S2.
(a) Calculate the initial charge acquired by
C1.
This I got to be 72μC
(b) Calculate the final charge on each capacitor.
This is where I am stuck...
Q1' = 72μC - Q2'
(72μC) - Q2'
___________ =
(4μF)
Q2'
____________
(7μF)
I know that I am supposed to solve for Q2' at this point but I don't know how.
Can someone please please help me??
Once I find Q2' then I can find Q1 by taking (72μC) - (Q2)...correct??
(a) Calculate the initial charge acquired by
C1.
This I got to be 72μC
(b) Calculate the final charge on each capacitor.
This is where I am stuck...
Q1' = 72μC - Q2'
(72μC) - Q2'
___________ =
(4μF)
Q2'
____________
(7μF)
I know that I am supposed to solve for Q2' at this point but I don't know how.
Can someone please please help me??
Once I find Q2' then I can find Q1 by taking (72μC) - (Q2)...correct??
Last edited: