Equation of Motion of Mass Damper and Rotating Bar

[ThLiOp]

Homework Statement

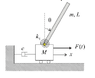
Consider the inverted pendulum system, where a uniform rigid bar of mass m and length L is elastically hinged on top of a lumped mass M. The bar is constrained by a torsional spring of coefficient kτ and the mass is constrained by a damper of coefficient c. Derive the nonlinear equations of motion for the system by the Newtonian Method.

The Attempt at a Solution

I have drawn the FBD of each mass and got the separate equations of motion:

For mass M:
M$\ddot{x}$+c$\dot{x}$ = F(t)

For rotating bar:
J$\ddot{θ}$+k$_{τ}$$\dot{θ}$ = 0

where J = (1/3)mL$^{2}$, resulting in

(1/3)mL$^{2}$$\ddot{θ}$+k$_{τ}$$\dot{θ}$ = 0

I am not sure how to relate the 2 in order to derive the nonlinear EOM. Any hints or suggestions would be greatly appreciated!

 

[KataKoniK]

Thank you for your post. To derive the nonlinear equations of motion for this system, we can use the Newtonian method by considering the forces and torques acting on each mass and applying Newton's second law.

For the lumped mass M, we have the equation of motion:

M\ddot{x}+c\dot{x} = F(t)

For the rotating bar, we can use the moment of inertia J = (1/3)mL^{2} and the torque equation:

J\ddot{θ}+k_{τ}\dot{θ} = -T(t)

Where T(t) is the external torque acting on the bar. To relate the equations of motion for each mass, we can use the relationship between linear and angular acceleration:

a = r\ddot{θ}

Where r is the distance from the pivot point to the center of mass of the bar. Therefore, we can rewrite the equation for the bar as:

(1/3)mL^{2}\ddot{θ}+k_{τ}\dot{θ} = -rT(t)

We can then combine this equation with the equation for the lumped mass by substituting in the relationship between linear and angular acceleration:

M\ddot{x}+c\dot{x} = -rT(t)

This gives us a set of coupled nonlinear equations of motion for the system. I hope this helps. Let me know if you have any further questions or need clarification.