Evaluating a momentum operator

[JD_PM]

Homework Statement

Show that the momentum operator $\hat{\vec P}$ yields



$$\hat{\vec P} = \int d^3 \vec x \frac{1}{c^2} \mathcal{N} \left( \dot A_{\mu} \nabla A^{\mu} \right) = \sum_{\vec k} \hbar \vec k N( \vec k)$$



Where $\mathcal{N}$ stands for normal-ordering and $N( \vec k)$ is the number operator

$N( \vec k) = \sum_{r=0}^3 \zeta_r a_r^{\dagger} (\vec k) a_r^{\dagger} (\vec k)$ (for instance, EQ $5.33$ Mandl & Shaw)

Relevant Equations

Please see below

I think I get the approach. We first need to evaluate the term $\dot A_{\mu} \nabla A^{\mu}$ and then evaluate the 3D space integral; we may need to take the limit $V \rightarrow \infty$ (i.e $\sum_{\vec k} (2 \pi)^3/V \rightarrow \int d^3 \vec k$) at some point.

The mode expansions of the vector potential $A^{\mu}=A_{+}^{\mu} + A_{-}^{\mu}$ are

$$A_{-}^{\mu}=\sum_{r=0}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r^{\dagger}(\vec k) e^{ik \cdot x} \right] \tag{1.1}$$

$$A_{+}^{\mu}=\sum_{r=0}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r(\vec k) e^{-i \vec k \cdot \vec x} \right] \tag{1.2}$$

The time-derivatives of $(1.1)$ and $(1.2)$ are

$$\dot A_{-}^{\mu} = ik^0 e^{ik^0 x^0}\sum_{r=0}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r^{\dagger}(\vec k) e^{-i \vec k \cdot \vec x} \right]$$

$$\dot A_{+}^{\mu} = -ik^0 e^{-ik^0 x^0}\sum_{r=0}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r(\vec k) e^{i \vec k \cdot \vec x} \right]$$

The spatial-derivatives of $(1.1)$ and $(1.2)$ are

$$ \nabla A_-^{\mu} = -i e^{ik^0 x^0}\sum_{r=0}^3 \sum_{\vec k} \left[ \vec k \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r^{\dagger}(\vec k) e^{-i \vec k \cdot \vec x} \right]$$

$$ \nabla A_+^{\mu} = i e^{-ik^0 x^0}\sum_{r=0}^3 \sum_{\vec k} \left[ \vec k \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r(\vec k) e^{i \vec k \cdot \vec x} \right]$$

We evaluate $\dot A_{\mu} \nabla A^{\mu}$

$$\dot A_{\mu} \nabla A^{\mu}=(\dot A^{+}_{\mu}+ \dot A^{-}_{\mu})(\nabla A_+^{\mu} +\nabla A_-^{\mu})=\dot A^{+}_{\mu}\nabla A_+^{\mu} + \dot A^{-}_{\mu}\nabla A_-^{\mu} + \dot A^{+}_{\mu}\nabla A_-^{\mu}+\dot A^{+}_{\mu}\nabla A_+^{\mu}$$

Let's evaluate $\dot A^{+}_{\mu}\nabla A_+^{\mu}$ explicitly

$$\dot A^{+}_{\mu}\nabla A_+^{\mu}=-ik^0 e^{-ik^0 x^0}\sum_{r=0}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \eta_{\mu \nu} \epsilon_r^{\nu} a_r(\vec k) e^{i \vec k \cdot \vec x} \right]i e^{-ik^0 x^0} \sum_{r=0}^3 \sum_{\vec k} \left[ \vec k \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \epsilon_r^{\mu} a_r(\vec k) e^{i \vec k \cdot \vec x} \right] \tag{*}$$

OK $(*)$ looks messy; let's focus on relevant terms

$$\dot A^{+}_{\mu}\nabla A_+^{\mu} \sim \eta_{\mu \nu} \epsilon_r^{\nu} a_r(\vec k) \vec k \epsilon_r^{\mu} a_r(\vec k)= \eta_{\mu \nu} \epsilon_r^{\nu} \vec k \epsilon_r^{\mu} a_r(\vec k) a_r(\vec k)\tag{**}$$

Once here, based on the orthonormality and completeness of the polarization vectors

And the customary choice of polarization vectors

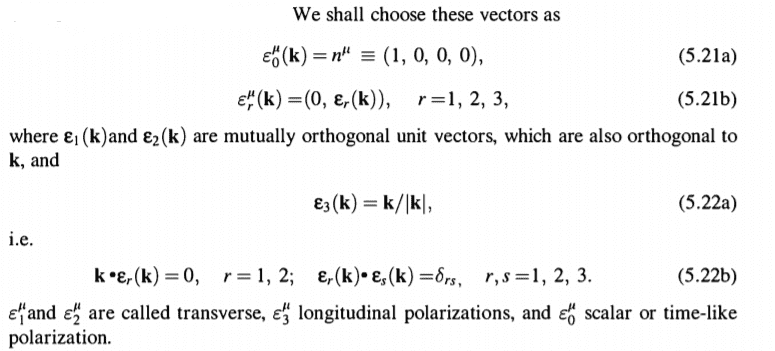
So the idea would be using $(5.19)$ but we do not have the $\zeta_r$ factor. Besides, the 3-vector $\vec k$ suggests we may have to use the orthogonal conditions $(5.22b)$.

How could we evaluate $(*), (**)$ then?

Thank you

 

[vanhees71]

It's a pretty longish calculation. You have to be a bit more careful though when looking at products and use different momenta for each of the factors and then interchange the momentum integrals with the spatial integral making use of
$$\int_{\mathbb{R}^3} \mathrm{d}^3 x \exp(\mathrm{i} (\vec{k}_1-\vec{k}_2) \cdot \vec{x})=(2 \pi)^3 \delta^{(3)}(\vec{k}_1-\vec{k}_2).$$
Then you can do one of the then trivial momentum integrations and are left with the other momentum integral leading to the right-hand side of the formula you want to prove. Just keep calculating!

 

[JD_PM]

Hi vanhees71, I see it better now thanks to your comments.

OK let me rewrite $(*)$, distinguishing momentum and polarization vectors. I also noticed I missed a $1/c$ factor (which pops up due to $\partial_{0}=\partial/(c\partial t)$)

$$\dot A^{+}_{\mu}\nabla A_+^{\mu}=\sum_{r,s=0}^3 \sum_{\vec k, \vec k'} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \Big(\frac{\hbar c^2}{2V \omega_{\vec k'}} \Big)^{1/2} k^0/c \ \eta_{\mu \nu} \epsilon_r^{\nu}(\vec k) a_r(\vec k) e^{-i k \cdot x} \vec k' \epsilon_s^{\mu}(\vec k') a_s(\vec k') e^{-i k' \cdot x} \right]$$

$$=\sum_{r,s=0}^3 \sum_{\vec k, \vec k'} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \Big(\frac{\hbar c^2}{2V \omega_{\vec k'}} \Big)^{1/2} k^0/c \ \vec k'\epsilon_{r \mu}(\vec k)\epsilon_s^{\mu}(\vec k') a_r(\vec k) a_s(\vec k') e^{-i (k+k') \cdot x} \right]$$

Using the orthonormality condition $(5.18)$ and $k^0 = \omega_{\vec k} / c$

$$=-\sum_{r,s=0}^3 \sum_{\vec k, \vec k'} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \Big(\frac{\hbar c^2}{2V \omega_{\vec k'}} \Big)^{1/2} k^0/c \ \vec k'\zeta_r \delta_{r,s}\delta_{\vec k, \vec k'} a_r(\vec k) a_s(\vec k') e^{-i (k+k') \cdot x} \right]$$ $$=-\sum_{r}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar }{2V} \Big) \vec k \zeta_r a_r(\vec k) a_r(\vec k) e^{-2i k \cdot x} \right]$$

Mmm this (at least) smells good! We've got the $\hbar \vec k$ term and $\zeta_r$. However there are two main issues: I do not get the number operator and $e^{-2i k \cdot x}$ is not the expected factor (we would expect something like $e^{i (k-k') \cdot x}$, so that the Dirac-delta function could be obtained after integrating over momentum space).

I considered the possibility that this term may not contribute to the final answer but I do think it does, as none of the other 3 terms is $\sim a_r(\vec k) a_r(\vec k)$...

Or maybe I just need to think more about it

 

[vanhees71]

You forgot the $\vec{x}$-integral. Only then the resulting $\delta^{(3)}(\vec{k}+\vec{k}')$ allows you to use the orthonormality condition for the polarization vectors but then also you have the factor $\vec{k}$!

 

[JD_PM]

You forgot the $\vec{x}$-integral

Oh I see! Let's try again

$$\frac{1}{c^2} \int d^3 \vec x \sum_{r,s=0}^3 \sum_{\vec k, \vec k'} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \Big(\frac{\hbar c^2}{2V \omega_{\vec k'}} \Big)^{1/2} k^0 \ \vec k'\epsilon_{r \mu}(\vec k)\epsilon_{s}^{\mu}(\vec k') a_r(\vec k) a_s(\vec k') e^{-i (k+k') \cdot x} \right]=$$

$$= \frac{1}{c^2} \sum_{r,s=0}^3 \sum_{\vec k, \vec k'} \left[ \Big(\frac{\hbar c^2}{2V \omega_{\vec k}} \Big)^{1/2} \Big(\frac{\hbar c^2}{2V \omega_{\vec k'}} \Big)^{1/2} k^0 \ \vec k'\epsilon_{r \mu}(\vec k)\epsilon_{s}^{\mu}(\vec k') a_r(\vec k) a_s(\vec k') (2 \pi)^3 \delta^{(3)}(\vec k + \vec k') e^{-i (k^0+k'^0) x}\right] \tag{@}$$

Where I've performed the 3D integral. Taking the limit $V \rightarrow \infty$ (i.e $\sum_{\vec k} (2 \pi)^3/V \rightarrow \int d^3 \vec k$) and the orthonormality condition $(5.18)$ we get

$$@ = \frac{1}{c^2} \sum_{r,s=0}^3 \sum_{\vec k} \int d^3 \vec k' \left[ \Big(\frac{\hbar c^2}{2 \omega_{\vec k}} \Big)^{1/2} \Big(\frac{\hbar c^2}{2 \omega_{\vec k'}} \Big)^{1/2} k^0 \ \vec k'\epsilon_{r \mu}(\vec k)\epsilon_{s}^{\mu}(\vec k') a_r(\vec k) a_s(\vec k') \delta^{(3)}(\vec k + \vec k') e^{-i (k^0+k'^0) x}\right]=$$

$$= \sum_{r,s=0}^3 \sum_{\vec k} \left[ \Big(\frac{\hbar }{2} \Big) \vec k \ \epsilon_{r \mu}(\vec k)\epsilon_{s}^{\mu}(\vec k) a_r(\vec k) a_s(\vec k) e^{-i (k^0+k'^0) x}\right]=$$

$$= -\frac{\hbar }{2} \sum_{r=0}^3 \sum_{\vec k} \left[ \vec k \
\zeta_r a_r(\vec k) a_r(\vec k) e^{-i (k^0+k'^0) x}\right]$$

Mmm it does not look right, as I am not getting the number operator, I get the extra factor $e^{-i (k^0+k'^0) x}$ and the -ive sign.

I have the same issue with the term

$$\dot A^{-}_{\mu}\nabla A_-^{\mu} \sim -a_r^{\dagger} (\vec k) a_r^{\dagger} (\vec k)$$

Thinking...