Inverse of a multivariate function

[docnet]

Homework Statement

Find the inverses of the given map F.

Relevant Equations

F(x)=y with y = 4x^3-3x

F(u,v) = (x,y) with (x=u^2-v^2, y=2uv)

Any help with this introductory differential geometry HW would be greatly appreciated.

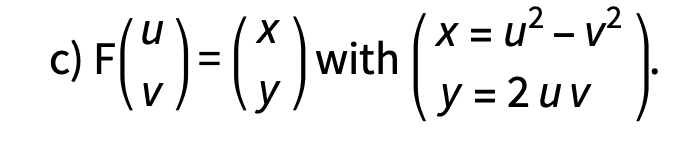
My attempt at solving the first problem:

y=4x^3-3x has the derivative 12x^2-3, which is 0 when x^2=(1/4). {x^2=(1/4)} is the singular set, and the inverse is defined for everywhere except F({x^2<(1/4)}). the image of F inverse does not include the singular set. there are three inverses for -1/2>x>1/2, x<1/2 and x>1/2. All my attempts to find the inverse of F(x) did not give me a solution. The calculator tells me a complicated answer.

Second problem:

the derivative of the map has the determinant 4u^2+4v^2, which is 0 when u=-v. I substituted v=-u into y=2uv, and found u= +/-sqrt(-y/2). then I substituted u back into y=2uv and found v. However, the resulting equation for v and u do not give back y when plugged into y=2uv. It gives back x when plugged into y=u^2-v^2 though. something is wrong. There are four inverses corresponding to the plus/minus signs for u and v. the image of the inverse of F does not contain the singular set {u=-v}. The inverse is not defined for {x=0, y<0} and the the conditions for x and y that makes the solutions for u and v undefined. thank you in advance for any pointers.

 

[vela]

For a), try plotting y=F(x).

the derivative of the map has the determinant 4u^2+4v^2, which is 0 when u=-v.

Are you sure about that?

 

[pasmith]

For (c): Set $(u,v) = (r \cos \theta, r \sin \theta)$ and recall that $$\begin{align*} \cos 2\theta &= \cos^2 \theta - \sin^2 \theta \\ \sin 2\theta &= 2\cos\theta \sin \theta \end{align*}$$

 

[benorin]

Alternatively if you don't mind complex numbers, $F(u+iv)=(u+iv)^2$ for part c). The previous suggestion is the equivalent of polar form of complex numbers of course.

 

[epenguin]

For the first inverse you say the calculator gives you only complicated things. That's because the algebraic solution just is complicated. Though an algebraic solution can be given but it's the one you probably obtained from the computer. This is true not just because somebody told you – you could possibly reason this out.In your efforts you possibly thought the right hand side is not all that complicated, maybe there is some trick of manipulation you could find that neatly gives you a solution. But think, it involves solving (getting the answer x = something) a cubic equation in x in which the constant term is y. The only seeming simplification is that the coefficient of the x² term is 0. But that is not much of a simplification – you can change by simple linear substitution this coefficient in any cubic into a 0. So if that made it simple, solving any cubic would be simple. Note that this clever thing you hope for has to work for all y. Too much to ask. On the other hand you could probably find a thing that falls out simply for some special values of y - for instance 0, or ½ or -½. But actually you already know the solutions for this so that doesn't have much value.

What you are clearly meant to do with this question is to remember the identity

cos 3x = 4 cos³x - 3 cosx

Which you may or may not have seen or studied before, if not or if forgotten check it out, used in the trick called "Trigonometrical solution of the cubic".

 

[docnet]

thank you to all that replied.

trick called "Trigonometrical solution of the cubic".

thank you. I had given up after trying to solve this problem for a week. This trick gave me the three inverse functions restricted to lyl<1, which is a whole lot better than nothing.

For (c): Set $(u,v) = (r \cos \theta, r \sin \theta)$ and recall that $$\begin{align*} \cos 2\theta &= \cos^2 \theta - \sin^2 \theta \\ \sin 2\theta &= 2\cos\theta \sin \theta \end{align*}$$

Thank you. I made the substitutions and got y/x = tan2Θ Am I correct to guess that a trigonometric identity involving tan2Θ should be applied here? at which stage does the information give back the inverse map in terms of x and y?

 

[docnet]

Alternatively if you don't mind complex numbers, $F(u+iv)=(u+iv)^2$ for part c). The previous suggestion is the equivalent of polar form of complex numbers of course.

Can you elaborate? I am not sure how complex numbers will be applied here, due to my inexperience of working with them.

 

[docnet]

For (c): Set $(u,v) = (r \cos \theta, r \sin \theta)$ and recall that $$\begin{align*} \cos 2\theta &= \cos^2 \theta - \sin^2 \theta \\ \sin 2\theta &= 2\cos\theta \sin \theta \end{align*}$$

ok, I spent more time on this problem. The trig substitution shows the map rotates a point in the xy plane around the origin by double the angle of the point in the uv plane.

After trig substitution we get y/x = tan2Θ

which means (1/2) arctan (y/x) = Θ

Θ = arctan(v/u) and I am not sure how to proceed.

 

[benorin]

$F(u+iv)=(u+iv)^2\Rightarrow F^{-1}(u,v)=(u+iv)^{\tfrac{1}{2}},F^{-1}(u,v)=(-u-iv)^{\tfrac{1}{2}}$ since the square root is multi-valued.

 

[docnet]

$F(u+iv)=(u+iv)^2\Rightarrow F^{-1}(u,v)=(u+iv)^{\tfrac{1}{2}},F^{-1}(u,v)=(-u-iv)^{\tfrac{1}{2}}$ since the square root is multi-valued.

I sort of see how F(u+iv) = u^2-v^2 + 2uvi corresponds to the multivariate function in the problem. the real part is x and the imaginary part y.

I don't see how to make F-1= (u+iv)^1/2 useful. could you explain?

 

[docnet]

Solved!

These problems were assigned by R. Hamilton, a person who is known for having discovered the Ricci flow.

If we do trig substitutions, we shows the function relates every point on the uv plane with a point on the xy plane by the angle Θ. the angle Θ is defined by the below expressions.

v/u = tanΘ, tan2Θ = y/x

combining these two expressions gives back y = 2uv and x = u^2-v^2. so perhaps trig substitution is not useful nor the complex number equivalent. What this doesn't tell us is the map rotates by an angle Θ and the distance from the origin becomes squared. I should have seen this by simply plotting points, but I only used points that are unit distance from the origin. so I missed the squaring factor.

We can show that u^2+v^2 = sqrt(x^2+y^2)
and since u^2-v^2 = x
we can treat these as a system of equations and solve for u and v.

which gives u = sqrt{[x+sqrt(x^2+y^2)]/2}
and v = sqrt{[-x+sqrt(x^2+y^2)]/2}

Also solving the equations y = 2uv and x = u^2-v^2 by substitution works. It gives eight equivalent sets of answers for u and v, with the signs next to the entire terms, distance terms and the x's reversed.

We plug in u = y/uv into x = u^2-v^2, solve the quartic equation 4u^4 - rxu^2 - y^2=0, and plug in v into x = u^2-v^2 to get the results. This gives every set of answers. However, only this sequence of substitutions gave the correct results. Various other substitutions led to wrong answers. (I wonder how?)

 

[epenguin]

thank you. I had given up after trying to solve this problem for a week. This trick gave me the three inverse functions restricted to lyl<1, which is a whole lot better than nothing.

Yes, a whole lot better. It works for the case of three real roots of the cubic. When there is only one real root, i.e. outside the range you mention then the corresponding identity for the hyperbolic function $cosh$ $3x$ works.

You might find it amusing (and possibly instructive, well you are past that but many students find it difficult to get the idea of inverse functions) if you have a graphing calculator, to plot the function and plot the inverse function that you find, and see how one is the same as the other rotated and reflected. Use the same scale for x and y axes of course.If possible post your graphs here. (And certainly state your results, see my sig.)

 

[docnet]

Yes, a whole lot better. It works for the case of three real roots of the cubic. When there is only one real root, i.e. outside the range you mention then the corresponding identity for the hyperbolic function $cosh$ $3x$ works.

You might find it amusing (and possibly instructive, well you are past that but many students find it difficult to get the idea of inverse functions) if you have a graphing calculator, to plot the function and plot the inverse function that you find, and see how one is the same as the other rotated and reflected. Use the same scale for x and y axes of course.If possible post your graphs here. (And certainly state your results, see my sig.)

Thank you. I was able to find three inverse functions of y=4x^3-3x and their graphic representations. I'll update with the work soon :)