Temperature profile between two parallel plates

[skrat]

Homework Statement

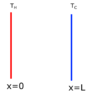
Imagine two parallel plates at distance $L$. One of them at constant temperature $T_H$ and the other one at $T_C$. Media between the plates is air.

Find $T$ as function of distance from the plate with $T_H$ in steady state.

Homework Equations

Navier - Stokes
Heat transfer
Mass continuity

The Attempt at a Solution

So I started with Navier Stokes

$\rho \frac{\partial T(x)}{\partial t} + \rho \nabla \cdot (\vec v\vec v) = - \nabla P + \nabla (\mu \nabla \vec v) + \vec b$

where I assumed steady state and no external body force. In addition to that I assumed pressure $P$ is constant, therefore

$\rho \nabla \cdot (\vec v\vec v) = \nabla (\mu \nabla \vec v).$

Rewritten in one dimension, that is

$\frac{\partial ^2 v}{\partial x^2}-\frac{\rho}{\mu}\frac{\partial v}{ \partial x} = 0$

The one dimensional heat equation in steady state should be

$\rho c_p\frac{\partial}{\partial x} (T(x)v(x)) = \lambda \frac{\partial ^2}{\partial x^2}T(x)$

ASSUMING everything is ok until here, I'm not sure how to solve these two DE. Any hints?

 

[Chestermiller]

You forgot to mention that you have axial flow with velocity v, correct. Which direction is the flow direction, x, y, or z? Which direction is perpendicular to the plates? Is the flow steady state?

 

[skrat]

The only flow there is a result of natural convection. And yes, I am only interested in steady state solutions.

The whole idea of this problem is to study the thermal layer. As a result I should be able to see that the higher the difference between $T_H$ and $T_C$ the thinner the thermal layer gets. Or something similar to that.

 

[Chestermiller]

The only flow there is a result of natural convection. And yes, I am only interested in steady state solutions.

View attachment 240182

The whole idea of this problem is to study the thermal layer. As a result I should be able to see that the higher the difference between $T_H$ and $T_C$ the thinner the thermal layer gets. Or something similar to that.

You never mentioned that the plates are vertical. What is the boundary condition at large distances high up and at large distances low down? What do you think the temperature and vertical velocity are at the centerline? What would the temperature profile be if there were no natural convection?

 

[skrat]

I did not mention the plates are vertical, because I wanted to avoid any gravitational effect. Yet I see now how this is wrong.

Plates are infinitely large. The temperature at the centerline is something between $T_H$ and $T_C$. Velocity is probably zero there.

If there were ne natural convection the profile would be linear.

 

[Chestermiller]

I can help you through this. But we have to proceed my way. What does your intuition tell you about the velocity in the x (horizontal direction)? What does your intuition tell you about the velocity in the vertical direction?

 

[skrat]

I'm not sure about the horizontal component, I'd say it's zero. Vertical component tho (magnitude) should be very large close to the plates but 0, or very close to 0, in between.

Correct?

 

[Chestermiller]

You are correct about the horizontal component.

The vertical component is zero at the plates and at the centerline; it is upward in the half of the channel next to the hot plate and is downward in the half of the channel next to the cold plate. And, because the system is infinite in the vertical direction, the vertical velocity does not vary with vertical position.

Now that you know that the horizontal velocity is zero, what does your steady state heat equation from post #1 give you for the temperature probile?

 

[skrat]

I hope I'm getting this right, but a general heat equation is

$\rho c_p\frac{\partial T}{\partial t} + \rho c_p \nabla (T \vec v) = \lambda \nabla ^2 T.$

Steady state problem and mass coninuity ($\nabla \cdot \vec v = 0$) yields

$\rho c_p \vec v \nabla T = \lambda \nabla ^2 T$

or in cartesian coordinates

$\rho c_p v_y(x)\frac{\partial T(x)}{\partial x} = \lambda \frac{\partial ^2 T(x)}{\partial x^2}.$

So tells me about nothing since I don't know the $v_y(x)$.

 

[Chestermiller]

$\rho c_p v_y(x)\frac{\partial T(x)}{\partial x} = \lambda \frac{\partial ^2 T(x)}{\partial x^2}.$

So tells me about nothing since I don't know the $v_y(x)$.

This is incorrect. It should read
$$\rho c_p v_y(x)\frac{\partial T}{\partial y} = \lambda \frac{\partial ^2 T}{\partial x^2}$$
and we have that $\frac{\partial T}{\partial y}=0$

 

[skrat]

A, sorry, I was too fast.

$\rho c_p \frac{\partial T}{\partial t} + \rho c_p \nabla( T\vec v) = \nabla(\lambda \nabla T)$

because we are only interested in steady state, where $\frac{ \partial T}{\partial t} =0$ then

$\rho c_p \nabla \cdot( T\vec v) = \nabla \cdot (\lambda \nabla T).$

Now if I am not mistaken $\nabla \cdot (\psi \vec a) = \psi \nabla \cdot \vec a + \vec a \cdot \nabla \psi$ which than yields

$\rho c_p [T\nabla \cdot \vec v + \vec v \cdot \nabla T] = \nabla \cdot (\lambda \nabla T).$

Now considering mass continuity $\nabla \cdot \vec v = 0$ and assuming $\lambda$ is constant

$\rho c_p \vec v \cdot \nabla T = \lambda \nabla ^2 T.$

So yes, exactly what you say it should be.

To answer your question: Solution to that DE is a linear function. Integrating

$\frac{\partial ^2 T}{\partial x^2} = 0$

twice, gives me

$T(x)= Ax + B.$

Applying boundary conditions $T(x = 0) = T_H$ and $T(x = L) = T_C$ finally reads

$T(x) = (T_C - T_H)\frac{x}{L} + T_H$Which is not what I was expecting. I was expecting to see something similar to figure 3 here: http://e6.ijs.si/~jslak/files/papers/CP_2018_KosecSlak_ICCM.pdf You also mentioned the upward and downward flow next to the plates.

 

[Chestermiller]

A, sorry, I was too fast.

$\rho c_p \frac{\partial T}{\partial t} + \rho c_p \nabla( T\vec v) = \nabla(\lambda \nabla T)$

because we are only interested in steady state, where $\frac{ \partial T}{\partial t} =0$ then

$\rho c_p \nabla \cdot( T\vec v) = \nabla \cdot (\lambda \nabla T).$

Now if I am not mistaken $\nabla \cdot (\psi \vec a) = \psi \nabla \cdot \vec a + \vec a \cdot \nabla \psi$ which than yields

$\rho c_p [T\nabla \cdot \vec v + \vec v \cdot \nabla T] = \nabla \cdot (\lambda \nabla T).$

Now considering mass continuity $\nabla \cdot \vec v = 0$ and assuming $\lambda$ is constant

$\rho c_p \vec v \cdot \nabla T = \lambda \nabla ^2 T.$

So yes, exactly what you say it should be.

To answer your question: Solution to that DE is a linear function. Integrating

$\frac{\partial ^2 T}{\partial x^2} = 0$

twice, gives me

$T(x)= Ax + B.$

Applying boundary conditions $T(x = 0) = T_H$ and $T(x = L) = T_C$ finally reads

$T(x) = (T_C - T_H)\frac{x}{L} + T_H$Which is not what I was expecting. I was expecting to see something similar to figure 3 here: http://e6.ijs.si/~jslak/files/papers/CP_2018_KosecSlak_ICCM.pdf You also mentioned the upward and downward flow next to the plates.

Well, for the problem as you stated it, this is the solution for the temperature profile. This exact problem is solved in Transport Phenomena by Bird, Stewart, and Lightfoot. The calculated temperature profile will generate upward flow in the half of the channel next to the hotter plate, and downward flow in the half of the channel next to the colder plate.

 

[skrat]

Hmmm. Makes sense. Looks like my inuition is closer to time dependant solution rather than steady state.

Would it be very hard to find the $T(x, t)$?

 

[Chestermiller]

Hmmm. Makes sense. Looks like my inuition is closer to time dependant solution rather than steady state.

Would it be very hard to find the $T(x, t)$?

Would it not be the same as the solution to the transient heat conduction equation without any flow?

 

[skrat]

Would it not be the same as the solution to the transient heat conduction equation without any flow?

You see that's what I don't understand and that's why I believe the solution should not be the same. The media between the plates is fluid (e.g. air at atmospheric pressure). While conductive heat transfer is transfer of energy by vibrations at molecular level thorough a solid or fluid, the convective heat transfer is a mechanism occurring because of bulk motion of fluids.

So in case of a plate at $T_H$ and another one at $T_C$ and assuming the media in between has $T_0 = \frac 1 2 (T_H + T_C)$ the transient temperature profile should really be different. Since the plates are infinitely large, I would still expect only the $T(x)$ dependency but for sure not linear (except in steady state). Rather than linear the temperature close to the hotter wall should be high (because of the air flow rising from below) and then it should drop close to $T_0$. Close to the colder wall there should be a similar effect. Similar to the velocity magnitude.

So what I want to see is the effect of convective heat transfer. Thinking about it, maybe my OP question is wrong. Maybe I should be studying the velocity as a function of x and $\delta T = T_H - T_C$ rather than $T(x)$. That way I could see the thickness of thermal layers in the transient heat transfer.

 

[Chestermiller]

You see that's what I don't understand and that's why I believe the solution should not be the same. The media between the plates is fluid (e.g. air at atmospheric pressure). While conductive heat transfer is transfer of energy by vibrations at molecular level thorough a solid or fluid, the convective heat transfer is a mechanism occurring because of bulk motion of fluids.

So in case of a plate at $T_H$ and another one at $T_C$ and assuming the media in between has $T_0 = \frac 1 2 (T_H + T_C)$ the transient temperature profile should really be different. Since the plates are infinitely large, I would still expect only the $T(x)$ dependency but for sure not linear (except in steady state). Rather than linear the temperature close to the hotter wall should be high (because of the air flow rising from below) and then it should drop close to $T_0$. Close to the colder wall there should be a similar effect. Similar to the velocity magnitude.

So what I want to see is the effect of convective heat transfer. Thinking about it, maybe my OP question is wrong. Maybe I should be studying the velocity as a function of x and $\delta T = T_H - T_C$ rather than $T(x)$. That way I could see the thickness of thermal layers in the transient heat transfer.

Well, what you're saying doesn't make sense to me personally, but that's why we have equations to help us work this all out. So the first thing you should do (before getting into the transient problem) is to solve the steady state problem for the velocity distribution. Why? Because if you can't solve that, you certainly won't be able to solve the transient problem. Plus, you will be getting some added insights as to the effects (or non-effects) of convection in this system and the relative magnitudes of the upward and downward velocities. So, are you interested in quantifying that solution? If not, you can just look it up in Transport Phenomena.