Gh778
- 419
- 0
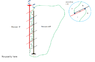
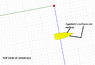
I try to find the movement of classic helicoids and the sum of energy with 3 different pressures. For me when two identical helicoids turn in the same direction around their axis, they don't move up/down. In fact, when I see helicoids turning I see all static except the helicoid which turn around their axis. Like all is static, for me, it's possible to put pressure 3*P everywhere outside black helicoid except between helicoids where pressure is 2*P. And for red helicoid it's possible to P pressure everywhere outside except between helicoids. The difference of pressure want to turn each helicoid in the same direction. Green separation is there for prevent 3*P pressure to go to P pressure area, this area is static. If helicoids turn they give energy, but like I loss nothing in energy, I think the system can't turn like that or the pressure can't be put like that but I don't know where is the problem here. Sure there are a lot of gaskets, not show on the drawing.
Edit: the green area can be smaller and can be attach to the black helicoid with gaskets.
Edit: helicoids turn at the same speed
Edit: In fact, I see the film with pressure 2P move up (or down), this film can be very small because helicoïds have same pitch, think with internal thread (female) and external thread (male) there is no space between helicoids. Here helicoids are joined at external in a small part but enough for create a torque.
Edit: The intersection of helicoids is a line so maybe the surface is 0. But think with only one interface with 2P pressure, we can oriented helicoids for have a greater surface, one helicoid on Z axis and other make an angle like 2*pitch.
Edit: the green area can be smaller and can be attach to the black helicoid with gaskets.
Edit: helicoids turn at the same speed
Edit: In fact, I see the film with pressure 2P move up (or down), this film can be very small because helicoïds have same pitch, think with internal thread (female) and external thread (male) there is no space between helicoids. Here helicoids are joined at external in a small part but enough for create a torque.
Edit: The intersection of helicoids is a line so maybe the surface is 0. But think with only one interface with 2P pressure, we can oriented helicoids for have a greater surface, one helicoid on Z axis and other make an angle like 2*pitch.
Attachments
Last edited: