Water Pressure at the tap and practical Bernoulli equation

[fog37]

TL;DR Summary

How to apply Bernoulli eqn to a real life scenario

Hello,
I think I understand how Bernoulli equations works but I am clearly uncertain on some aspects of its application. For example, let's look at the figure below:

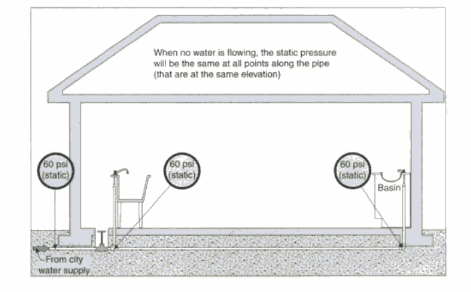
1) The static pressure is $60$ $psi$ from the city water supply. There is not flow (tap closed) so the pressure at the either basin is also $60psi$ regardless of the the pipe length, diameter, internal friction, number of bends/turns. We can measure that pressure, when the water is not moving, using pressure gauges.

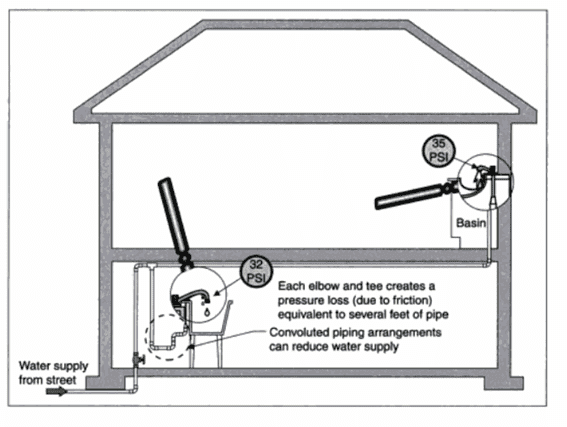
2) Now we open the tap at one of the basis and water starts flowing. The pressure from the city water supply is still $60$ $psi$. But the pressure along the pipe decreases due to a) friction, b) pipe bends/curves, c) elevation changes, so the pressure at either basin\ is $p<60$ $psi$.

Questions
1) Shouldn't the water pressure $p$ be equal to atmospheric pressure at the tap of each basis where the water exists? Why not? Why is the pressure $35$ $psi$ at the tap of the top basin and is not equal to atmospheric pressure?
2) In the ideal case (no friction, no bends, no elevation changes), the pressure at the basins would also be equal to $60$ $psi$ even when the water flows (not just in the static case) and the tap is open, correct? There would be a sharp pressure discontinuity at the tap, with pressure going from #60## $psi$ to atmospheric pressure...
3) The flow rate (gallons/minute) is determined by pipe's cross-sectional area $A$ and speed $v$ at the tap (I think).
What is the role of tap pressure (downstream)? The larger the tap pressure the larger the flow rate? Or what matters is only the water pressure upstream at the water supply from the street (bottom left)?
For example, let's assume the same pipe diameter, length, friction, and same pressure upstream ($60$ $psi$) but a different pressure downstream at the tap. How does that affect the flow rate? Is the flow rate lower? Why?

Thank you!Thank you!

 

[jrmichler]

The pressure gauge at the tap is probably located a few inches upstream from the valve. That valve typically has a small opening for water to flow, there are normally several changes of direction in the tap, plus an aerator at the discharge end. All of that stuff between the pressure gauge and the discharge makes for a relatively large resistance to flow. So the pressure drops from 60 PSI at the street, to 35 PSI just before the valve, and 0 PSI at the discharge. It drops from 35 PSI to 0 PSI over a short distance because there is a lot of resistance to flow in that short distance.

The flow rate is determined by the total resistance to flow. If you increase size of the line from the street to the valve, the pressure at the tap will increase from 35 PSI to something closer to 60 PSI. The new flow will be approximately proportional to the square root of the ratio of the new pressure to the old pressure.

If you built a water system with pipes large enough to deliver 60 PSI to the discharge nozzle, then the water would be coming out fast enough to cause injury. I did something similar once when I made a nozzle with a 1.0 mm hole, and put it on the end of a garden hose. The hose was so much larger than the nozzle opening that it delivered the full 50 PSI city water pressure to the nozzle. It would shoot a narrow jet of water over the roof of the house. The force of the jet on my finger convinced me that a kid could injure themself with it. So I destroyed the nozzle.

 

[tnich]

The Venturi effect would also come into play when you open the tap. The increase (from zero) in the velocity of the water through the pipe would be accompanied by a decrease in pressure.

 

[fog37]

The pressure gauge at the tap is probably located a few inches upstream from the valve. That valve typically has a small opening for water to flow, there are normally several changes of direction in the tap, plus an aerator at the discharge end. All of that stuff between the pressure gauge and the discharge makes for a relatively large resistance to flow. So the pressure drops from 60 PSI at the street, to 35 PSI just before the valve, and 0 PSI at the discharge. It drops from 35 PSI to 0 PSI over a short distance because there is a lot of resistance to flow in that short distance.

The flow rate is determined by the total resistance to flow. If you increase size of the line from the street to the valve, the pressure at the tap will increase from 35 PSI to something closer to 60 PSI. The new flow will be approximately proportional to the square root of the ratio of the new pressure to the old pressure.

If you built a water system with pipes large enough to deliver 60 PSI to the discharge nozzle, then the water would be coming out fast enough to cause injury. I did something similar once when I made a nozzle with a 1.0 mm hole, and put it on the end of a garden hose. The hose was so much larger than the nozzle opening that it delivered the full 50 PSI city water pressure to the nozzle. It would shoot a narrow jet of water over the roof of the house. The force of the jet on my finger convinced me that a kid could injure themself with it. So I destroyed the nozzle.

Hello jrmichler,

Thank you. So what you mean is that, assuming low internal resistance, and if the pipe was of uniform diameter, the pressure downstream would almost equal to the pressure of 60 psi upstream. If you go from the diameter $D$ to a smaller diameter $d<D$, with that pressure, the speed of flow would be very large and possibly hurtful, correct?

I have seen a book example about a fire-hose tip: the pressure in the 6.4 cm diameter section is about 50 psi and speed is 4 m/s. Using the continuity equation, the speed in the narrower 2.5 diameter section is 26.2 m/s and the pressure is reduced to 20 psi.

Once the fluid stream exits the hose, the diameter of the stream just outside the fire hose tip is slightly smaller (instead of larger. Why?) so the speed becomes higher, 26.8 m/s, and the pressure is not atmospheric pressure...

In solving problems like the one with a hole on the side of a container filled with water, we know the pressure at a certain depth is larger than atmospheric pressure by a factor $\rho g y$. So why do set the pressure at the hole equal to atmospheric pressure $p_0$ and not equal to $p_0+ \rho g y$?

 

[jrmichler]

Be careful with the fire hose (pun intended - I (barely) hung onto a fire hose once). The pressure immediately outside the hose nozzle tip is atmospheric pressure. If you know the velocity, you can work your way upstream and calculate what the pressure would be without friction. Remember that one of the assumptions behind the Bernoulli Equation is zero friction. As you work calculate your way upstream, you will eventually get a point of known pressure. The actual pressure will be higher than your calculated pressure because of friction.

When working with typical residential / commercial / industrial / fire fighting water applications where the pressure is on the order of 50 PSI, and the point of discharge is within a few vertical feet of the source, it is easy to just ignore the effect of static head. Not completely correct, but good enough in the real world.

The container with a hole is different. There is no pump, just the effect of gravity. So the pressure immediately downstream from the hole is $p_o$, while the pressure immediately upstream is $p_o + \rho gy$. The velocity pressure is equal to the difference between those two pressures. Mathematically, those two points are "close" together, in the real world the upstream point is at least one hole diameter upstream from the hole.

 

[fog37]

So, at the inlet, the typical pressure is about 60 psi and then it is decreased, intentionally, at the various faucets on the home, shower, etc. What is the typical pressure? Around 40 psi? I am sure it depends on the type of sink, etc.
This 40 psi pressure is the water pressure just before water exits the faucet. Once the water stream is out of the faucet, its pressure become atmospheric pressure which is about 15 psi. Is that correct?

When the faucets are closed (no water flowing) the pressure is about 60 psi at every faucet on the first floor and lower than 60 psi at the higher floors, correct?

 

[jrmichler]

Be careful. There are two ways of measuring pressure:

Absolute pressure is the pressure relative to a vacuum. Atmospheric pressure is 14.7 PSIA (Pounds per Square Inch Absolute) at sea level under standard conditions.

Gauge pressure is what you read on a typical pressure gauge. It is referenced to the local atmospheric pressure. A pressure gauge connected to nothing setting on the table reads zero because it is zero PSI above the local atmospheric pressure.

If the local atmospheric pressure is about 15 PSIA, then the water stream pressure will be:

At the header: 75 PSIA or 60 PSIG
In the tap: 55 PSIA or 40 PSIG
Out of the tap: 15 PSIA or 0 PSIG

It is technically correct to use either PSIA or PSIG, but it is typical to use PSIG for water flow, and PSIA for compressible gas flow.

When the faucets are closed (no water flowing) the pressure is about 60 psi at every faucet on the first floor and lower than 60 psi at the higher floors, correct?

Yes.

 

[fog37]

Thank you, you are right, I should have specified gauge (relative) pressure. The mentioned pressures of 60 psi and 40 psi are indeed gauge pressure in excess of atmospheric pressure which has an absolute pressure of 15 psi...

Why do we call these pressures "static" pressures even when the fluid is flowing? I understand that "dynamic" pressure, one the terms in Bernoulli eqn, is just the extra contribution to static pressure p that we would get if the flow was brought to rest to a stagnation point. However, the the water is flowing out of the faucet, its pressure $p$ just before it exits is indeed termed static pressure...That seems confusing.

There is fundamentally only one pressure, which is $p$, and is called static pressure. It is the same as hydrostatic pressure when the liquid is at rest...

 

[fog37]

On a different note, what instrument would I use to measure the water pressure of the water at the tap opening when the tap is open? A gauge manometer on the tap would block the flow and not measure the pressure at the tap when the water is flowing...Would that be a Venturi tube?

 

[jrmichler]

The static pressure at the tap opening is zero PSIG because the water stream is open to atmosphere. The velocity pressure is higher, and can be measured with a pitot tube (search the term).

If the inside of the tap is a tube of constant diameter, then the static pressure a short distance upstream from the opening will be very close to zero, and the velocity pressure will be the same as at the opening.

 

[fog37]

Thank jrmichler.

In thread #7, you mention the following:

At the header: 75 PSIA or 60 PSIG: ok
In the tap: 55 PSIA or 40 PSIG: this is pressure right before water exits the tap with the tap open
Out of the tap: 15 PSIA or 0 PSIG: ok

For example, on the first floor, this means that the water pressure at the water supply inlet is about 60 psi.
However, the water pressure at a basin also on the first floor, when the tap is open, is 15 psi (once the water stream is out in the air). But, because of losses and the fact that water has a velocity, the water pressure at the tap, a little bit before it exits, is decreases to 55 or 40 psi as you mention. How do I measure that pressure? The 55 psi is not the pressure when the tap is closed.

The Pitot tube serves to measure the flow speed which is what the Venturi flowmeter does too...