thedean515
- 11
- 0
Hi,
As you know the capacitance per unit length of a standard coaxial cable is
C_{coax} = \frac{2 \pi \varepsilon_{0} \varepsilon_{r}}{\ln{\frac{b}{a}}}
where b is the radius of the cable and a is radius of the central conductor.
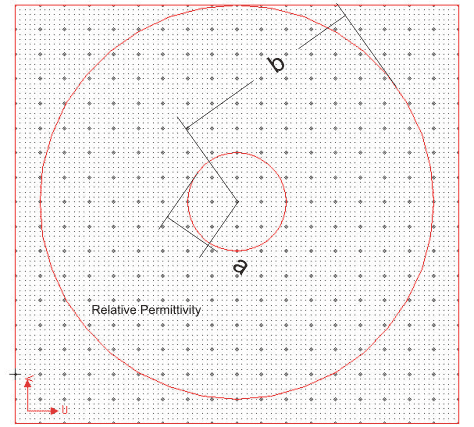 .
.
If we only want to know the capacitance of a quarter of the cable, it is just \frac{1}{4}C_{coax}
What if the cental conductor is off-set, how can we calculate the capacitance? Especiall I am interest to know the capacitance for only a quarter of the cable.
The off-set coax cable case is:
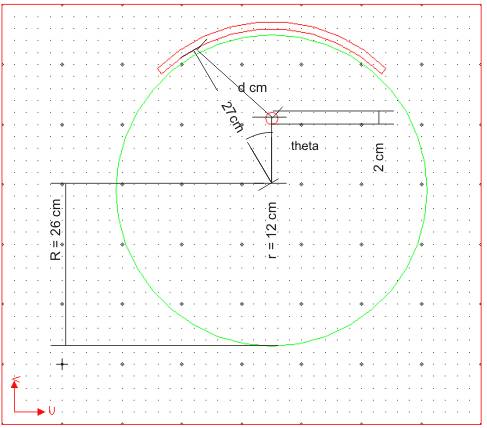
As you know the capacitance per unit length of a standard coaxial cable is
C_{coax} = \frac{2 \pi \varepsilon_{0} \varepsilon_{r}}{\ln{\frac{b}{a}}}
where b is the radius of the cable and a is radius of the central conductor.
If we only want to know the capacitance of a quarter of the cable, it is just \frac{1}{4}C_{coax}
What if the cental conductor is off-set, how can we calculate the capacitance? Especiall I am interest to know the capacitance for only a quarter of the cable.
The off-set coax cable case is: