idlackage
- 10
- 0
Homework Statement
Determine the angle of incline on https://www.physicsforums.com/attachment.php?attachmentid=30517&stc=1&d=1291856979" frictionless air track.
Acceleration = 0.147 m/s2.
The answer is supposed to be 4.10°.
Homework Equations
Fnet = ma
The Attempt at a Solution
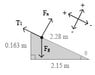
Mass 1 (https://www.physicsforums.com/attachment.php?attachmentid=30515&stc=1&d=1291856979"):
Perpendicular (y):
Fny = +Fn
Ty = 0
ay = 0
Fgy = -m1gcosθ
= (428)(-9.80)cosθ
= -4194.4cosθ
Fn + Fgy = 0
Fn = +4194.4cosθ
Parallel (x):
Fnx = 0
= -m1gxsinθ
= -4194.4sinθ
Fnet = m1a
Fn + Fgx + T = m1a
+4194.4cosθ – (-4194.4sinθ) + T
= (428)(0.147)
= 62.9
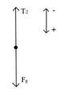
Mass 2 (https://www.physicsforums.com/attachment.php?attachmentid=30516&stc=1&d=1291856979"):
Fg2 = (20.0)(9.80)
= 196
Fg2 + T = m2a
196 + T = (20.0)(0.147)
= 2.94
T = 2.94 – 196
T = -490
Final calculations:
+4194.4cosθ – (-4194.4sinθ) + T = 62.9
(-) T = -490
----------------
+4194.4cosθ – (-4194.4sinθ) = 552
Not only do I not know how to solve that final equation, I'm also sure the answer will be wrong. I really don't get how to properly go about this question.
Attachments
Last edited by a moderator: