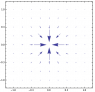
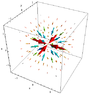
r[x_, y_, z_] := Sqrt[x^2 + y^2 + z^2]
\[CurlyPhi][x_, y_] := ArcTan[x, y]
\[Theta][x_, y_, z_] := ArcCos[z/Sqrt[x^2 + y^2 + z^2]]
(* Unit vectors *)
ex[x_, y_, z_] := Sin[\[Theta][x, y, z]] Cos[\[CurlyPhi][x, y, z]]
ey[x_, y_, z_] := Sin[\[Theta][x, y, z]] Sin[\[CurlyPhi][x, y, z]]
ez[x_, y_, z_] := Cos[\[Theta][x, y, z]]
(* Components of the Vector Field *)
Vx[x_, y_, z_] := -(1/r[x, y, z]^2) ex[x, y, z]
Vy[x_, y_, z_] := -(1/r[x, y, z]^2) ey[x, y, z]
Vz[x_, y_, z_] := -(1/r[x, y, z]^2) ez[x, y, z]
VectorPlot3D[{Vx[x, y, z], Vy[x, y, z], Vz[x, y, z]}, {x, -1,
1}, {y, -1, 1}, {z, -1, 1},
VectorPoints -> 5,
VectorStyle -> "Arrow3D", VectorColorFunction -> Hue,
AxesLabel -> {"x", "y", "z"}]