Understanding Special Relativity: Time Dilation and Space Contraction Explained

[blueberrynerd]

Hi! I've just began studying Special Relativity, so I'm naturally having trouble understanding some topics. I just need an opinion on whether my understanding of the topic is right or not.

I've been wondering how time dilation is connected to space contraction. For a relativistic moving frame, space contracts in the direction of motion and at the same time, light travels a greater distance and time accordingly slows down to account for the invariant value of c?

I'm just wondering if my understanding of the topic is correct. I'd really appreciate any input.

 

[BruceW]

That's right. Length contraction and time dilation are given by the more general Lorentz transform equations. These equations have the property that the speed of light is the same as measured by any reference frame

 

[BruceW]

To explain length contraction: let's say we have a ruler that we measure to be 1 meter when stationary, then if we measure its length while it is moving, it will be less than 1 meter.
and for time dilation: If we measure a clock to tick once every minute when stationary, then if we measure it while its moving, it will tick once every minute and a half (for example).

 

[blueberrynerd]

Thanks for the reply! :)

So could you say that time dilation and length contraction go hand-in-hand for a relativistic reference frame?

 

[blueberrynerd]

I also understand how the speed of light accounts for time dilation, but I don't understand how it leads to length contraction.

 

[BruceW]

In what way have you learned about how the speed of light accounts for time dilation?
When I first did relativity, my lecture explained to us a geometrical example, where a combination of time dilation and length contraction led to the speed of light being the same as measured by two different observers.

 

[blueberrynerd]

The way I understood it was that light appears to travel a longer path for an observer in a fixed reference frame and since c has to be constant, time appears to be lengthened as well.

 

[BruceW]

Your terminology isn't quite right, but I think you've got the right idea. At the heart of it all, the speed of light must be the same, so clocks and rulers will go slower/get shorter than if you measured them when they were stationary.
If you only allowed time dilation, and not length contraction, then it would not be possible to have the speed of light the same relative to all observers. This is why length contraction must happen.

 

[blueberrynerd]

Would it be correct to say that length contraction causes c to be constant while time dilation happens as a consequence of the invariance of c?

 

[bobc2]

Would it be correct to say that length contraction causes c to be constant while time dilation happens as a consequence of the invariance of c?

Blueberrynerd, I don't know if the space-time sketches will just make things more confusing or not, but some people find it easier to resolve a question like this by visualizing the relationships between different observers and between observers and objects in 4 dimensions. If you think of the four dimensions as X1, X2, X3, and X4, then you can suppress X2 and X3 in the diagrams so as to focus on how things relate in the X1-X4 coordinates. Here are some basic examples.

Looked at in this way you might think more about the consequence of a very mysterious and fundamental aspect of the relativistic 4-D space. If an observer is in motion with respect to a rest system, his X4 axis is rotated. Further, his X1 axis is rotated also such that a 4-D photon world line will always bisect the angle between the X4 and X1 axis. All observers move along their own X4 axis (their world line) at the speed of light. And since the photon world line is always at a 45 degree angle and bisects X4 and X1 for all observers (no matter their speed), then all observers will measure a ratio of 1:1 between the photon's distance traveled along X4 and distance traveled along X1. And of course the speed of light results from our convention for calibrating time along X4 (remember all observers move along X4 at light speed--although what aspect of the observer is actually doing the moving is a very protacted philosophical discussion not appropriate here).

So, I wouldn't put the cause for the relativistic phenomena squarely on the speed of light. It's more a consequence of the strange rotating of all observer's X4 and X1 axes. You see right away in the pictures below that different observers have different 3-D cross-section views of the 4-dimensional universe. The different geometric views result in different observations of times and distances when observing other observers in relativistic motion. I'm just trying to make the point that it is fruitful to study relativity in the context of geometry: 4-dimensions and 3-D cross-section views. You can google space-time diagrams to dig into this in much more detail.

 

[ghwellsjr]

Hi! I've just began studying Special Relativity, so I'm naturally having trouble understanding some topics. I just need an opinion on whether my understanding of the topic is right or not.

You are showing indications of not understanding Special Relativity. Look at these three comments of yours concerning frames:

For a relativistic moving frame, space contracts in the direction of motion and at the same time, light travels a greater distance and time accordingly slows down to account for the invariant value of c?

So could you say that time dilation and length contraction go hand-in-hand for a relativistic reference frame?

The way I understood it was that light appears to travel a longer path for an observer in a fixed reference frame and since c has to be constant, time appears to be lengthened as well.

You need to understand several things about reference frames in Special Relativity.

First off, you should think in terms of a single, stationary reference frame which we use to define the positions of observers and objects as a function of time. Observers and objects can be moving (or stationary), but not the frame. If an observer/object is stationary with respect to the reference frame, then its clocks tick at a normal rate and its rulers are all a normal length, no matter their orientations. If an observer/object is moving with respect to the reference frame, then its clocks tick at a slower rate (with a longer time interval) and its rulers are shortened along the direction of motion.

The speed of light is defined to be c in this single, stationary reference frame. It's fairly obvious that a stationary observer/object would be able to measure the speed of light to be c because its rulers and clocks are normal.

However, you need to know that in order to measure the speed of light, an observer can only measure the round trip speed of light. He needs to have a timing device located at the source of a flash of light and a mirrror some fixed distance away. He starts his timer when the flash is emitted and stops it when he sees the reflected light arrive back at his location. Then to calculate the speed of light, he takes double the distance divided by the time interval.

A moving observer will carry with him a moving light source, a moving timing device, and a moving mirror. Everything moves with respect to him so that for him, everything is stationary.

If he places his mirror in a direction that is at right angles to his direction of motion, then it will take longer for the light to leave the source, travel to the mirror, and reflect back to him. In this case, if his mirror is the same distance away as for the stationary observer, then all it takes is for his timing device to take a longer time per tick so that his measurement will come out the same as for the stationary observer. However, the stationary observer will observe him as taking longer than his own measurement.

If he places his mirror in a direction that is along his direction of motion, then it will also take longer for the light to leave the source, travel to the mirror, and reflect back to him, but if the distance to his mirror is the same as for the previous case, it will take even longer and he will not get the correct answer. For this reason, the distance has to be shortened by just the right amount so that he calculates c for the measured speed of light.

Now, it should also be understood that observers do not have to diliberately move their mirror closer or adjust the tick rate of their clock longer in order for them to measure the speed of light to be c, it happens automatically.

 

[BruceW]

Would it be correct to say that length contraction causes c to be constant while time dilation happens as a consequence of the invariance of c?

If we assume the invariance of c and the principle of relativity are correct, then: length contraction and time dilation must both be allowed. (So they are both a consequence of the invariance of c).
You could say it the other way round, and say that time dilation and length contraction can be used in special relativity to keep c the same as measured by all observers.

Edit: To make it clear, time and space are put on equal footing in relativity. The reason the lengths contract and time dilates is simply because of the way we define the 'proper length' and 'proper time'.

 

[JDoolin]

Hi! I've just began studying Special Relativity, so I'm naturally having trouble understanding some topics. I just need an opinion on whether my understanding of the topic is right or not.

I've been wondering how time dilation is connected to space contraction. For a relativistic moving frame, space contracts in the direction of motion and at the same time, light travels a greater distance and time accordingly slows down to account for the invariant value of c?

I'm just wondering if my understanding of the topic is correct. I'd really appreciate any input.

I'd say you are missing the vital third issue commonly known as the "relativity of simultaneity"

Imagine that you have an open-ceiling circular room ,filled with smoke (to reveal where a flash of light is), and walled with mirrors (to reflect the flash of light), and there is a bright flash of light that emits from the center, passes through the smoke in an expanding circle, bounces off walls (simultaneously), and arrives again simultaneously at the center.

From the point of view of someone hovering directly above the room, it appears that the light hits every part of the mirror simultaneously. However, to someone traveling past at 30% of the speed of light, it should appear as in the animation below.

There are three main differences from the hovering viewpoint and the .3c viewpoint:
(1) The light takes longer to make its outbound and return trip. (time dilation)
(2) The room no longer appears to be circular but slightly oval. (length contraction)
(3) The lignt no longer reaches all parts of the outer circle simultaneously, but instead hits the back end first. (relativity of simultaneity.)

 

[ghwellsjr]

JDoolin, your animation is fantastic. I wish I knew how to create such animations directly on a webpage. The only way I have known to do aminations is to capture them on youtube and point to them indirectly.

Your animation successfully illustrates the point you are making with regard to the relativity of simultaneity.

However, you should state that the views are not those of a person residing within the scenario but are rather for us outside the scenario as we observe what happens according to a defined FoR in which we do not have to worry about how long the image of an event that happens in the scenario takes to reach our eyes outside the scenario.

It's kind of like when we watch ripples on the surface of the water that travel at a very slow speed compared to the speed of light. If we were blind and had to rely on waiting until the water waves reflect off of objects and propagate back to us, we would then be in the same situation as a person in your scenario who won't be able to see the animation as you presented it.

Once you understand that, you will see that you don't need smoke in the room to reveal where the flash of light is because we know where it is based on our defined FoR in which we define the speed of light to be c. In fact, if you think about all the propagations of light within a smoke filled room, you will see that it just presents a lot of confusion because all the smoke lights up with reflections continuing to go in all directions. Nobody could actually see the scenario as you presented it.

But, like I say, take away the smoke and change the perspective from someone in the scenario to us outside the scenario who can observe instantly what is going on at each location within the scenario and you will have a great explanation to go with your great animation.

 

[JDoolin]

JDoolin, your animation is fantastic. I wish I knew how to create such animations directly on a webpage. The only way I have known to do aminations is to capture them on youtube and point to them indirectly.

Your animation successfully illustrates the point you are making with regard to the relativity of simultaneity.

However, you should state that the views are not those of a person residing within the scenario but are rather for us outside the scenario as we observe what happens according to a defined FoR in which we do not have to worry about how long the image of an event that happens in the scenario takes to reach our eyes outside the scenario.

It's kind of like when we watch ripples on the surface of the water that travel at a very slow speed compared to the speed of light. If we were blind and had to rely on waiting until the water waves reflect off of objects and propagate back to us, we would then be in the same situation as a person in your scenario who won't be able to see the animation as you presented it.

Once you understand that, you will see that you don't need smoke in the room to reveal where the flash of light is because we know where it is based on our defined FoR in which we define the speed of light to be c. In fact, if you think about all the propagations of light within a smoke filled room, you will see that it just presents a lot of confusion because all the smoke lights up with reflections continuing to go in all directions. Nobody could actually see the scenario as you presented it.

But, like I say, take away the smoke and change the perspective from someone in the scenario to us outside the scenario who can observe instantly what is going on at each location within the scenario and you will have a great explanation to go with your great animation.

Thank you very much. I made this animation about 10 years ago, I think, using gwbasic. I've long since forgotten how. There is a MUCH easier method now, if you have access to Mathematica:

http://academic2.american.edu/~jpnolan/Misc/MathematicaAnimation.html
Simply Export a Table of Graphics objects into a gif file.

And you're right. In the smoke example, "What you see" is not necessarily what you see in the animation. In fact, as the object is approaching from your left, it would appear elongated, and as it recedes to the right, it would appear even more contracted.

I suspect that if you are looking straight at it, though, as its path-of-motion crosses your line-of-sight at a 90° angle, a little small-angle-approximation could yield a proof that what you would see is at least "approximately" what is shown in the animation. The main concern is whether the speed of light delay is significantly different on the edges of the animation than in the center of the animation. If the object is passing at a distance far enough away, the difference between the path lengths is not significant, so the light from simultaneous events in that region would arrive (almost) simultaneously.


(P.S. Maybe we should want to eliminate the smoke and mirrors anyway, since "Smoke and mirrors is a metaphor for a deceptive, fraudulent or insubstantial explanation or description" http://en.wikipedia.org/wiki/Smoke_and_mirrors )

 

[ghwellsjr]

I suspect that if you are looking straight at it, though, as its path-of-motion crosses your line-of-sight at a 90° angle, a little small-angle-approximation could yield a proof that what you would see is at least "approximately" what is shown in the animation. (Edit: But since I neither offer nor link to such a proof, of course, you may doubt that such proof exists. I'm not sure I've ever actually seen such a proof, but I would be surprised if I were wrong.)

Yes, I doubt that a proof exists because it's not correct. The only way you could "solve" this problem is to have a whole bunch of observers above the scenario all spread out so that none of them has to do a small-angle-approximation and they each see delayed in time what is happening below them, but then you have the exact same problem of defining the time delays between them as you would for the observers in the scenario.

Just say that it is we as super observers outside the scenario who can "see" what is going on at any particular location inside the scenario in the "real time" of your FoR and the problem is solved.

 

[ghwellsjr]

(Edit: Maybe we should want to eliminate the smoke and mirrors anyway, since "Smoke and mirrors is a metaphor for a deceptive, fraudulent or insubstantial explanation or description" http://en.wikipedia.org/wiki/Smoke_and_mirrors )

Get rid of the smoke but you need the mirrors. You could place partial rings of mirrors of different diameters to let the observer in the center "observe" the progress of the light, but the main point is illustrating how both a stationary observer and a moving observer in any FoR both see themselves in the center of their set of mirrors.

 

[JDoolin]

In fact, if you think about all the propagations of light within a smoke filled room, you will see that it just presents a lot of confusion because all the smoke lights up with reflections continuing to go in all directions. Nobody could actually see the scenario as you presented it.

I'm not entirely sure I agree here. Do a google image search for spotlight smoke or light beam. The apparent location of the light doesn't really stray significantly outside the original region, which is controlled by the shape of the lens of the spotlight. There may be a few rare secondary reflections that would hit your eye, but very few, and far fewer still tertiary reflections.

 

[JDoolin]

Get rid of the smoke but you need the mirrors. You could place partial rings of mirrors of different diameters to let the observer in the center "observe" the progress of the light, but the main point is illustrating how both a stationary observer and a moving observer in any FoR both see themselves in the center of their set of mirrors.

Okay. Putting your observer "at the center" of the room would certainly ruin the "small-angle-approximation" that I was talking about before. My idea is to put both obserers (both the comoving observer, and the observer at .3c) far, far above the room.

You're right, that if you filled the room with smoke, and had the observer inside the room, imagining what that observer "sees" is going to be kind of tricky.

Yes, I doubt that a proof exists because it's not correct. The only way you could "solve" this problem is to have a whole bunch of observers above the scenario all spread out so that none of them has to do a small-angle-approximation and they each see delayed in time what is happening below them, but then you have the exact same problem of defining the time delays between them as you would for the observers in the scenario.

Just say that it is we as super observers outside the scenario who can "see" what is going on at any particular location inside the scenario in the "real time" of your FoR and the problem is solved.

Whoops, I edited my edit already, and then realized you had already replied. Sorry about that. I took out the part where I said "I didn't produce a proof", and put in:

The main concern is whether the speed of light delay is significantly different on the edges of the animation than in the center of the animation. If the object is passing at a distance far enough away, the difference between the path lengths is not significant, so the light from simultaneous events in that region would arrive (almost) simultaneously.​

It's may not pass for a formal proof, but it's pretty strong reasoning.

you have the exact same problem of defining the time delays between them as you would for the observers in the scenario.

I don't see any problem in defining the time delays. It's proportional to the distance from the events to the observer. So IF the distance to the events is approximately the same (as it would be if the observers were far above the room), THEN the time delay is the same, and the events which were simultaneous would appear approximately simultaneous... just delayed.

 

[BruceW]

The time delay due to transmission of speed of light is a problem in a lot of thought experiments.
Often in textbooks, they have to say 'measurements relative to a certain frame, when taking into consideration the delay due to transmission of light'.

 

[ghwellsjr]

Just because you are far away doesn't mean time delays become insignificant. It just means it's harder to actually see the image. You'd have to magnify it tremendously and it's those delays that carry the information to resolve the angles of the light from the different locations far below so that you can actually see what's going on.

Think about it a different way: Until you establish a timing convention, it's impossible to know the one-way speed of light which is necessary in order to build an image of where light is at any given moment. You're not going to trick nature into revealing this information to you by backing far away from the scenario.

That's why I say your animation is an excellent demonstration of what light does according to the timing convention established by Special Relativity for a particular Frame of Reference.

 

[ghwellsjr]

I'm not entirely sure I agree here. Do a google image search for spotlight smoke or light beam. The apparent location of the light doesn't really stray significantly outside the original region, which is controlled by the shape of the lens of the spotlight. There may be a few rare secondary reflections that would hit your eye, but very few, and far fewer still tertiary reflections.

You must have some magic smoke that doesn't attenuate the primary signal significantly but still provides a secondary reflection scattered in all directions but still bright enough to be detected far, far away. Comparison to a spotlight that's on all the time is not really the same. Imagine a flash bulb going off and you're far enough away from it that you can actually see the propagation of the flash through smoke. If the smoke scatters the light enough so that you can see it, it won't last long enough for you to see it hit the mirrors far enough away and reflect back to the origin.

Like I said, if you want to follow the progress, put in small mirrors at measured known distances, or just repeat the entire experiment with progressively larger circular rooms.

 

[JDoolin]

Think about it a different way: Until you establish a timing convention, it's impossible to know the one-way speed of light which is necessary in order to build an image of where light is at any given moment. You're not going to trick nature into revealing this information to you by backing far away from the scenario.

I was under the working assumption that the one-way speed of light is the same as the two-way speed of light; i.e.299 792 458 m/s. If an event happens at a point r away from you at time t, then you wll see that event at time T=t + r/c. Is that what you mean by a timing convention?

P.S. I'll see if I can put together a diagram here in a few minutes, and get a couple of calculations. Maybe I'll proof myself wrong.

PPS. I don't think I proved myself wrong, although I do see there is some interplay with the distance and the angle involved. If you have three simultaneous events (according to the observer) as pictured in the attached diagram, the time delay for the central event is

{Central Delay} = \frac{d}{c }

But the time delay for the events on either side are

{Edge Delay} = \frac{d}{c \cdot \cos(\theta)}

The difference in the delays, then would be {Difference} = \frac{d}{c }\left ( 1-\frac{1}{\cos(\theta)} \right )

So using, for instance d=1000 meters, θ=8°, you would have a field of view (2 d tan(θ)) 280 meters across with simultaneous events appearing no more than 30 nanoseconds apart. This is quite fast compared to the time it take light to travel across the field of view, ≈900 nanoseconds.

You can set the parameters of the thought experiment however you like. (how far away the observers are from the apparatus.) and choose the angle and distance so that (d/c)(1-1/cos(θ) is small relative to the time-scale of whatever phenomena you wish to measure.) (how long it takes light to travel across the circle).

 

[JDoolin]

You must have some magic smoke that doesn't attenuate the primary signal significantly but still provides a secondary reflection scattered in all directions but still bright enough to be detected far, far away. Comparison to a spotlight that's on all the time is not really the same. Imagine a flash bulb going off and you're far enough away from it that you can actually see the propagation of the flash through smoke. If the smoke scatters the light enough so that you can see it, it won't last long enough for you to see it hit the mirrors far enough away and reflect back to the origin.

Like I said, if you want to follow the progress, put in small mirrors at measured known distances, or just repeat the entire experiment with progressively larger circular rooms.

Okay. Putting in small mirrors at measured known distances, so they would reflect a porion of the light out to the observers, would work. Alternatively, we could invoke the "pragmatism immunity" common to all thought experiments, and say for this thought experiment, we use a "smoke that doesn't attenuate the primary signal significantly but still provides a secondary reflection scattered in all directions but still bright enough to be detected far, far away."

 

[ghwellsjr]

I was under the working assumption that the one-way speed of light is the same as the two-way speed of light; i.e.299 792 458 m/s. If an event happens at a point r away from you at time t, then you wll see that event at time T=t + r/c. Is that what you mean by a timing convention?

Yes, that's Einstein's timing convention and once you do that for your diagram, you have specified a Frame of Reference.

P.S. I'll see if I can put together a diagram here in a few minutes, and get a couple of calculations. Maybe I'll proof myself wrong.

PPS. I don't think I proved myself wrong, although I do see there is some interplay with the distance and the angle involved. If you have three simultaneous events (according to the observer) as pictured in the attached diagram, the time delay for the central event is

{Central Delay} = \frac{d}{c }

But the time delay for the events on either side are

{Edge Delay} = \frac{d}{c \cdot \cos(\theta)}

The difference in the delays, then would be {Difference} = \frac{d}{c }\left ( 1-\frac{1}{\cos(\theta)} \right )

So using, for instance d=1000 meters, θ=8°, you would have a field of view (2 d tan(θ)) 280 meters across with simultaneous events appearing no more than 30 nanoseconds apart. This is quite fast compared to the time it take light to travel across the field of view, ≈900 nanoseconds.

You can set the parameters of the thought experiment however you like. (how far away the observers are from the apparatus.) and choose the angle and distance so that (d/c)(1-1/cos(θ) is small relative to the time-scale of whatever phenomena you wish to measure.) (how long it takes light to travel across the circle).

So far, you are analyzing what a stationary observer sees of the stationary scenario below him. It's enough to point out that everything is symmetrical and therefore everything that the observer will see will look like circles.

But now you need to do this for the scenario for which you provided your animation, that is, of a moving observer. Your animation continues for four cycles of light expanding and collapsing and every one of them is identical. You could have continued this on forever, correct? But do you think the observer will continue to see the same thing forever? Isn't it obvious that eventually the angles for viewing each cycle will distort the image so that it doesn't match your animation? Once you see that, you can also see that there is distortion within each cycle right down to the very first one. That's all I'm trying to point out.

But again, just explain your animation as what a FoR defines for what happens without regard to delays caused by light propagation and you will have an accurate descriprtion for your great animation.

 

[ZealScience]

I think relativity implies that space and time cannot be separated. Change in space measurements affects time measurements. So I think that time dilation along with length contraction is intrinsic. I think in the 1916 paper on relativity, there was a derivation of the equations using space time one-to-one correspondence.

 

[BruceW]

That's sort of right. The Lorentz transforms essentially say that length and time measurements in one reference frame depend linearly on length and time measurements in another frame. So we can think of length and time as two axis, and changing to a different reference frame is like rotating this axis.
Time dilation is a special case of the Lorentz transform, where one of the reference frames measures zero spatial separation between two events.
And length contraction is a special case where one of the frames measures zero time difference between two events.

 

[JDoolin]

But do you think the observer will continue to see the same thing forever? Isn't it obvious that eventually the angles for viewing each cycle will distort the image so that it doesn't match your animation? Once you see that, you can also see that there is distortion within each cycle right down to the very first one. That's all I'm trying to point out.

No, the observer won't see the same thing forever. Yes, eventually the angles for viewing each cycle will distort the image. All I'm trying to say is that there is a region where the image is basically not distorted.

I realized this morning, that in order to explain where the image is not distorted, I have to first describe the nature of the distortion we expect, and then point out the region where the distortion is negligible.

The main axiom I'm using here is that the current apparent position of an object according to an observer, is the positional component (in the observer's current rest frame) of the intersection of the objects world-line (or curve) with the observer's current past light cone.

So the attached diagrams show first, a one-dimensional object passing in the y=0 plane. In this plane, the distortion is always present. In the second diagram, a one-dimensional object is passing in the y=d plane. In the y=d plane, there is a small region where there is no significant distortion between the "actual" length-contracted shape, and the "apparent" shape.

 

[ghwellsjr]

We both agree the distortion is at its minimum when the observer is directly overhead but it never goes away, even if you prefer to call it negligible.

But I don't recall you ever agreeing with me that there is zero distortion if you describe the animation as depicting what happens in the plane of the objects according to the observer's rest frame at all times in the past, present and future, and it doesn't matter how high the observer is above the objects. Agreed?

 

[JDoolin]

We both agree the distortion is at its minimum when the observer is directly overhead but it never goes away, even if you prefer to call it negligible.

Good. My main point is that Lorentz contraction and the relativity of simultaneity are things that a person could, at least in principle, observe directly.

But I don't recall you ever agreeing with me that there is zero distortion if you describe the animation as depicting what happens in the plane of the objects according to the observer's rest frame at all times in the past, present and future, and it doesn't matter how high the observer is above the objects. Agreed?

Yes, I agree, and I never meant to disagree on that point. But with one caveat:

(1) assuming that the events in the animation have been happening forever into the past, and into the future. The observer can only reconstruct events as they happened within his past light-cone.

However, I don't think this discussion can be put to rest just yet, because I recalled the reason I am chasing after this point so persistently. Because of a http://www.guspepper.net/electro/Segundo semestre/Seminarios/Funez.pdf" which determined that "the conformality of aberration ensures that, at least over small solid angles, each [co-located observer, regardless of relative speed] will see precisely what the other sees. No Lorentz contractions wll be visible, and all objects will appear normal."

 

[JDoolin]

However, I don't think this discussion can be put to rest just yet, because I recalled the reason I am chasing after this point so persistently. Because of a http://www.guspepper.net/electro/Segundo semestre/Seminarios/Funez.pdf" which determined that "the conformality of aberration ensures that, at least over small solid angles, each [co-located observer, regardless of relative speed] will see precisely what the other sees. No Lorentz contractions wll be visible, and all objects will appear normal."

It appears to me that Terrell is specifying an angle

\theta' = \cos^{-1}(v/c)

and perhaps at that particular angle, for an approaching object, the Lorentz contraction and the lengthening effect due to the time-delay cancel out. But in general, except for that one special case, I would expect the appearance of the object is distorted the entire time.

 

[ghwellsjr]

Yes, I agree, and I never meant to disagree on that point. But with one caveat:

(1) assuming that the events in the animation have been happening forever into the past, and into the future. The observer can only reconstruct events as they happened within his past light-cone.

I don't know why you think any restrictions are necessary. I only mentioned an observer because I wanted to provide continuity with your earlier description but we don't need an observer so let's just eliminate him. We are not concerned with any observer trying to reconstruct what happened in his past. We are just doing this from the definition of a Frame of Reference.

Let's first consider a Frame of Reference in which the scenario you described earlier is stationary (but without the smoke):

Imagine that you have an open-ceiling circular room ,filled with smoke (to reveal where a flash of light is), and walled with mirrors (to reflect the flash of light), and there is a bright flash of light that emits from the center, passes through the smoke in an expanding circle, bounces off walls (simultaneously), and arrives again simultaneously at the center.

If you had made an animation of this scenario, it would be just as you described it, an expanding circle of light simultaneously hitting all parts of the mirrored wall and collapsing back to the origin, repeating forever.

Now let's consider a new FoR that is moving at 0.3c with respect to the first FoR. Again, there is no observer in the scenario, just a light source and a circular wall of mirrors. Now your animation show exactly what is happening in this new FoR. Don't you agree?

 

[ghwellsjr]

The next thing I was going to have you consider, going back to your far away observers watching the scanario, is what would be the difference between your first observer "hovering directly above the room" and your second observer "traveling past at 30% of the speed of light". From far away, while the second observer is approximately directly above the room, can't you also say that his distortions will be negligible so that he sees approximately the same image that the stationary observer sees?

 

[JDoolin]

The next thing I was going to have you consider, going back to your far away observers watching the scanario, is what would be the difference between your first observer "hovering directly above the room" and your second observer "traveling past at 30% of the speed of light". From far away, while the second observer is approximately directly above the room, can't you also say that his distortions will be negligible so that he sees approximately the same image that the stationary observer sees?

The distortion would be a Lorentz contraction by a factor of \sqrt{1-\left(\frac{v}{c}\right)^2}=\sqrt{1-.3^2}=.954 compared to what the stationary observer sees.

Whether or not this is negligible is an opinion question, but I've been thinking of 1% difference as a cutoff for negligible. (which is why I used 8 degrees earlier in my calculation).

This would be a 4.6% difference which is above my cutoff, so I would say it is a significant (noticeable) difference from what the stationary observer would see. However, if you asked me to draw a circle free-hand, I imagine I would draw a circle which was even more distorted than 4.6%.

 

[ghwellsjr]

Now consider a stationary far away observer watching the room moving at 30% the speed of light. What would he see?

 

[JDoolin]

I don't know why you think any restrictions are necessary. I only mentioned an observer because I wanted to provide continuity with your earlier description but we don't need an observer so let's just eliminate him. We are not concerned with any observer trying to reconstruct what happened in his past. We are just doing this from the definition of a Frame of Reference.

Let's first consider a Frame of Reference in which the scenario you described earlier is stationary (but without the smoke):

If you had made an animation of this scenario, it would be just as you described it, an expanding circle of light simultaneously hitting all parts of the mirrored wall and collapsing back to the origin, repeating forever.

Now let's consider a new FoR that is moving at 0.3c with respect to the first FoR. Again, there is no observer in the scenario, just a light source and a circular wall of mirrors. Now your animation show exactly what is happening in this new FoR. Don't you agree?

I agree, but let me ask you another question: Can you construct an inertial reference frame without an origin? Can you describe the location and times of the events in an inertial reference frame without reference to some known and defined x = y = z = t = 0? And from that origin, for an inertial reference frame, there is a world-line extending through t along x=y=z=0.

You can get away without any observers in your reference frame, but you can't define a reference frame without placing an origin. And if you have to define an origin, doesn't it make sense to place it in a bird's-eye-view, where the effect we wish to describe is the most pronounced?

 

[JDoolin]

Now consider a stationary far away observer watching the room moving at 30% the speed of light. What would he see?

Are you serious? It's exactly the same scenario as your previous question. Exactly the same answer as post #34.

 

[ghwellsjr]

Terrell covers all these situations in the paper you linked to and in those cases where an object does not appear in its normal shape (distorted, in your words), it appears rotated rather than shortened to the degree required by Lorentz contraction. This is because of the fact that the image seen by the eye is not of the various parts of the object being viewed from the same distance to the eye and therefore not of the same time delay, and therefore not simultaneous, which is a requirement for measuring the correct Lorentz contraction.

I believe you have misunderstood Terrell's paper:

It appears to me that Terrell is specifying an angle

\theta' = \cos^{-1}(v/c)

and perhaps at that particular angle, for an approaching object, the Lorentz contraction and the lengthening effect due to the time-delay cancel out. But in general, except for that one special case, I would expect the appearance of the object is distorted the entire time.

He's not talking about an approaching object in your quote of the equation and he's not saying that something happens at just one particular angle. He's saying that in all cases, Lorentz contraction is never visible--note the title: Invisibility of Lorentz Contraction.

You might want to read this:

http://en.wikipedia.org/wiki/Penrose-Terrell_rotation

 

[ghwellsjr]

I don't know why you think any restrictions are necessary. I only mentioned an observer because I wanted to provide continuity with your earlier description but we don't need an observer so let's just eliminate him. We are not concerned with any observer trying to reconstruct what happened in his past. We are just doing this from the definition of a Frame of Reference.

Let's first consider a Frame of Reference in which the scenario you described earlier is stationary (but without the smoke):

If you had made an animation of this scenario, it would be just as you described it, an expanding circle of light simultaneously hitting all parts of the mirrored wall and collapsing back to the origin, repeating forever.

Now let's consider a new FoR that is moving at 0.3c with respect to the first FoR. Again, there is no observer in the scenario, just a light source and a circular wall of mirrors. Now your animation show exactly what is happening in this new FoR. Don't you agree?

I agree, but let me ask you another question: Can you construct an inertial reference frame without an origin? Can you describe the location and times of the events in an inertial reference frame without reference to some known and defined x = y = z = t = 0? And from that origin, for an inertial reference frame, there is a world-line extending through t along x=y=z=0.

You can get away without any observers in your reference frame, but you can't define a reference frame without placing an origin. And if you have to define an origin, doesn't it make sense to place it in a bird's-eye-view, where the effect we wish to describe is the most pronounced?

It's no different than the typical animations of a moving one-dimensional light clock which show two moving mirrors with a photon or light flash bouncing along diagonals between them. Your animation is just a moving two-dimensional circular light clock. What's the difference? Why do you have to be so rigorous when nobody else is? People talk all the time about Frames of Reference in very general terms even to the point of saying "the rest frame of an observer" as if there is only one. They even draw sketches of scenarios all the time without worrying about those details. It really only matters if you want to do a rigorous Lorentz Transform on the scenario when you have to be very precise.

"And if you have to define an origin, doesn't it make sense to place it in a bird's-eye-view, where the effect we wish to describe is the most pronounced?"​

I don't understand this at all. Even if you defined an origin in your animation along with axes labels and a definition of time, where is the effect most pronounced and what has that got to do with a bird's-eye-view?

 

[JDoolin]

I'd still like some feedback from this last quote. Why don't you just describe your animation as what is happening in a Frame of Reference to your moving circular room?

My point was not to attack your explanation, but to defend my own. As long as you acknowledge that, yes, there are specific positions where you could place a camera where the Lorentz Contraction and relativity of simultaneity would be seen as shown, then you can explain it however you want.

I think it is less confusing to invoke an actual position from which you're watching the events unfold, and describe what you would see from that position.


[PLAIN]http://www.psychologytoday.com/files/u248/long_hallway_JeffK.jpg
I decided to throw in this image for good measure. What is "really happening in this frame of reference" is describable in four dimensions. But your perspective is still important. And in my animation, there is an implied perspective, which is straight-on. Just claiming that "this is what is really going on" implies that there is some way of visualizing things without a perspective. Philosophically, I don't really believe there is such a thing. A reference frame without an observer, is one that no one is imagining. It's an ambiguous and undefinable construct. If you're imagining a reference frame, you have to imagine it from a perspective.

 

[ghwellsjr]

First off, let me appologize for completely changing my previous post which you just quoted. I hadn't realized when I composed it that you had already provided the feedback I requested and I thought I could then respond to your feedback before you had a chance to see my unnecessary duplicate request. But I appreciate this further feedback which I will respond to now.

My point was not to attack your explanation, but to defend my own. As long as you acknowledge that, yes, there are specific positions where you could place a camera where the Lorentz Contraction and relativity of simultaneity would be seen as shown, then you can explain it however you want.

I'm not convinced that it's possible to place a camera anywhere that would show Lorentz Contraction and relativity of simultaneity, especially after you pointed out Terrell's article and he was just talking about the shape of a solid object. When it comes to tracking the expanding circle of light, I'm really not convinced that there is any way to take a picture of it that would look like your animation and that's not because of the smoke issue. To me, it's the same issue as two observers, moving with respect to each other "observing" the same expanding circle of light that started when they were colocated, who will both correctly determine that they continue to be in the center of that expanding circle, even though they are no longer colocated. So it seems to me that the camera is just another observer that would simply record an image of the expanding circle of light that showed the camera always in the center and so it would be incapable of showing the expanding circle of light in a different location from the collapsing circle of light or the point of reflection sweeping around the mirrored wall. But I could be wrong.

I think it is less confusing to invoke an actual position from which you're watching the events unfold, and describe what you would see from that position.

Well, as I pointed out in my first post on this subject, Frames of Reference are made for us, outside of the scenario, to actually observe. No one inside the scenario can possibly actually see what we illustrate in a FoR.

[PLAIN]http://www.psychologytoday.com/files/u248/long_hallway_JeffK.jpg
I decided to throw in this image for good measure. What is "really happening in this frame of reference" is describable in four dimensions. But your perspective is still important. And in my animation, there is an implied perspective, which is straight-on. Just claiming that "this is what is really going on" implies that there is some way of visualizing things without a perspective. Philosophically, I don't really believe there is such a thing. A reference frame without an observer, is one that no one is imagining. It's an ambiguous and undefinable construct. If you're imagining a reference frame, you have to imagine it from a perspective.

I'm not following this at all, sorry. A FoR is a perspective. And it's just one of an infinite number of equivalent FoRs. None of them is claiming that "this is what is really going on" if by that you mean what is really going on in nature. But within any FoR it's legitmate to say what is really going on in that FoR, by definition, I might add.

 

[JDoolin]

Terrell covers all these situations in the paper you linked to and in those cases where an object does not appear in its normal shape (distorted, in your words), it appears rotated rather than shortened to the degree required by Lorentz contraction. This is because of the fact that the image seen by the eye is not of the various parts of the object being viewed from the same distance to the eye and therefore not of the same time delay, and therefore not simultaneous, which is a requirement for measuring the correct Lorentz contraction.

I believe you have misunderstood Terrell's paper:

He's not talking about an approaching object in your quote of the equation and he's not saying that something happens at just one particular angle. He's saying that in all cases, Lorentz contraction is never visible--note the title: Invisibility of Lorentz Contraction.

You might want to read this:

http://en.wikipedia.org/wiki/Penrose-Terrell_rotation

I think this is the relevant question: Is the Lorentz contraction "invisible" as Terrell claims, or has James Terrell made a mistake which has gone unnoticed for decades?

I'll take some time to analyze Terrell's argument, and check whether my own methods (analyzing intersections of world-lines and light-cones) agree with his, (transformations of angles via an aberration equation) and if they don't agree, see if I can figure out why.

 

[formal]

That's right. Length contraction and time dilation are given by the more general Lorentz transform equations.

Is there any particular reason why transform must follow the curve of (co)secant?
Could you suggest a link?
Thanks

 

[JDoolin]

I think this is the relevant question: Is the Lorentz contraction "invisible" as Terrell claims, or has James Terrell made a mistake which has gone unnoticed for decades?

I'll take some time to analyze Terrell's argument, and check whether my own methods (analyzing intersections of world-lines and light-cones) agree with his, (transformations of angles via an aberration equation) and if they don't agree, see if I can figure out why.

(My method)

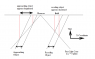
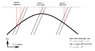
Consider a ruler lying in the y=1 plane and the z=0 plane. Consider marks on the ruler at points (-2.0, -1.9, -1.8, -1.7, ... 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6). (You can imagine the ruler going on forever if you prefer.

Assume your position is x=0,y=0,z=0, and the time is now t=0. (This experiment will take a long time to discuss, but essentially takes zero time to perform.) Assume also that the ruler is aligned with its zero mark at x=0 (with you).

Now, you are observing several "events" on the ruler. Namely, light bounced off or emitted from the ruler sometime in the past, and you are now seeing those events which happened in the past. You can calculate when those events happened by the formula:

t=-\frac{\sqrt{x^2+y^2}}{c}

Now we consider another observer passing through the same location and time (0,0,0,0) but traveling at a speed of 0.8c. The two of you share past light-cones, so all of the events that you are observing, the other observer is observing at the same instant.

However, to find out where he is seeing these events, we must perform a lorentz transformation on each of them.

\begin{align*} t' &= \gamma t - \beta \gamma x\\ x'&=-\beta \gamma t + \gamma x \\ \end{align*}

When this is done, in particular, the ruler marks (-1.5, -1.4, -1.3, -1.2, -1.1, -1.0) are mapped to new positions:

-0.0963, -0.0394, 0.0202, 0.0827, 0.1488, 0.2190

We are particularly interested in the markers -1.4 and -1.2, which now appear at positions -.0394 and .0827. The uncontracted length of the ruler is (-1.2) - (-1.4) = 0.2, while the apparent length is .0827 - (-.0934)=.1221 The length contraction factor is .1221/.2=.6105

Which is roughly* the same as that which is expected by the lorentz contraction factor \sqrt{1-0.8^2}= 0.6

*If you wanted more fine detail, you should make more marks on the ruler around x=-1.33


Terrell derived an aberration equation from the Lorentz transformations, then uses the aberration equation to conclude that the Lorentz contraction effect "vanishes," but I find it suspicious, when by using the Lorentz transformations directly, I find that the Lorentz contraction is quite visible.

I am attaching a couple of spreadsheet files (Excel, or openoffice, or import them into google-docs), so you can see how I calculated things. But I think that Terrell's statement that the Lorentz Contraction is "invisible" is definitely wrong. At this point, it's just a matter of figuring out exactly what his mistake was.

 

[JDoolin]

Is there any particular reason why transform must follow the curve of (co)secant?
Could you suggest a link?
Thanks

The Lorentz Transformation has events move along arcs of x^2 - (c t)^2 = constant.

I'm not sure where you're getting a "(co)secant" from. These are hyperbolic arcs.

You might find https://www.physicsforums.com/showpost.php?p=3405177&postcount=20" helpful.

 

[ghwellsjr]

"Roughly"?? If you did it right you would get exactly the same number.

You have transformed a number of events from one frame to another frame and then used the distance difference in that second frame to "see" the contraction but this is the wrong way to do it. Your mistake is in this sentence:

The two of you share past light-cones, so all of the events that you are observing, the other observer is observing at the same instant.​

An event that is transformed from one frame to another frame is no longer "at the same instant" just like it is no longer at the same location. Comparing just the spatial distance between two events in one frame with the spatial distance between the same two events in another frame will not give you the lorentz contraction. What you have to do is calculate two events in the second frame that have the same time coordinates and then take the spatial difference between them. This means that you will have to interpolate between a pair of events. If you do that, you will get exactly the correct lorentz contraction.

But beyond that, when you use the Lorentz Transform two describe events in a new FoR, you are doing what I said will produce the correct interpretation of your animation. A FoR does not describe what a stationary observer in that FoR actually sees. It only describes what we can determine is happening according to the definition of that FoR. No observer that we define to be in the FoR can actually see anything happening remotely to their location, they can only see what is happening locally to them and then it doesn't matter what FoR we choose as they will all disclose the same images for every observer.

Terrell is not saying that the length contraction is not happening, he is just saying that in order to "observe" it (using his distinction between "observe" and "see"), the extra time delay caused by light having to travel extra distance must be taken into account so that the events at the source must all be "observed" at the same instant in time. This of course is impossible to do with any optical equipment, its something that take has to be done by calculation.

 

[formal]

I'm not sure where you're getting a "(co)secant" from.

I considered C = 1 the hypotenuse and v/C one cathetus I got
sq.rt 1- v^2/ C^2 = *(co)sine and ( * )^-1 = (co)secant.
Or does this transform apply only to mass increase?

 

[JDoolin]

"Roughly"?? If you did it right you would get exactly the same number.

We've already talked about this. I thought we had agreed that the effect will at a minimum at a certain angle, but would never competely go away.

You can get it as exact as you want by using events around the point t'=-1, x'=0

<br /> \begin{pmatrix} <br /> c t&#039;\\ x&#039; <br /> \end{pmatrix} <br /> = \Lambda ^{-1} <br /> <br /> \begin{pmatrix} <br /> c t\\ x <br /> \end{pmatrix} <br /> <br />

<br /> = <br /> \begin{pmatrix} <br /> \gamma &amp; \beta \gamma \\ <br /> \beta \gamma &amp; \gamma <br /> <br /> \end{pmatrix}<br /> <br /> \begin{pmatrix} <br /> -1\\ 0 \end{pmatrix} = \begin{pmatrix} -\gamma\\ -\beta \gamma <br /> \end{pmatrix}<br />

Since in this case,
\begin{matrix} \beta = 0.8 \\ \gamma = \frac{1}{\sqrt{1-.8^2}}=\frac{5}{3}\\ \beta \gamma = \frac{4}{3} \end{matrix}

You can use points on the ruler right around x=-4/3, labeled, for instance 1.333 and -1.334, (and the corresponding t values, which you can easily calculate, using - (ct)^2 = x^2 + y^2
) .

You have transformed a number of events from one frame to another frame and then used the distance difference in that second frame to "see" the contraction but this is the wrong way to do it. Your mistake is in this sentence:

The two of you share past light-cones, so all of the events that you are observing, the other observer is observing at the same instant.​

An event that is transformed from one frame to another frame is no longer "at the same instant" just like it is no longer at the same location.

You are missing the point. Your statement is exactly correct.

However, I did not claim that the events were at the same location. I claimed that the light-cone contains the same events, but at different times and different locations. (Are you able to access the spreadsheet information?)

Maybe I should clarify that I am talking about the SURFACE of the light cone. I think the point you're missing is that the surface of the past light-cone with its point at (0,0,0,0) is the locus of events which can be detected at the event (0,0,0,0). This fact remains the same, regardless of the observer's reference frame.

No observer that we define to be in the FoR can actually see anything happening remotely to their location, they can only see what is happening locally to them and then it doesn't matter what FoR we choose as they will all disclose the same images for every observer.

I hope you can understand that the observer can see the locus of events on the surface of his or her past light-cone. The tip of the light-cone is the event where the information arrives. It is not a remote event, but THE local event. Naturally, it is also the one event which does not move when you perform a lorentz transformation. All of the other events move, but any event which is in the surface of the past light-cone stays in the surface of the past light-cone.

(If you have any doubt on this, think, how could it be otherwise? How could light that is arriving at an event (0,0,0,0) in one reference frame be NOT arriving at the event (0,0,0,0); the same exact event, in another reference frame? Also you can check the before and after transformation coordinates in my spreadsheet files, to check that indeed t' = -sqrt(x'^2+y'^2).)

 

[JDoolin]

I considered C = 1 the hypotenuse and v/C one cathetus I got
sq.rt 1- v^2/ C^2 = *(co)sine and ( * )^-1 = (co)secant.
Or does this transform apply only to mass increase?

Hmmm, maybe think of it with the slopes involved.

cosine(θ) = adjacent/hypotenuse = \frac{\Delta x}{\sqrt{\Delta x^2+\Delta y^2}} = \frac{1}{\sqrt{1 + \left( \frac {\Delta x}{\Delta y} \right )^2}}

where θ=arctan(y/x)

hyperbolic cosine (φ)= gamma = (time component)/(space-time-interval)

\frac{\Delta t}{\sqrt{\Delta t^2-\Delta x^2}} = \frac{1}{\sqrt{1 - \left( \frac {\Delta x}{\Delta t} \right )^2}}

where φ=arctanh(x/t)



P.S. sqrt(1-x^2) is only the cosine of an angle assuming that x^2 is the sine of an angle, right?

 

[formal]

Hallo Sir, thanks for your attention ( I was greatly impressed by your applet!)
I repeat : I was referring to relativistic-mass, and don't know for sure how this relates to time-dilation/space-contraction

I consider triangle AOB with angle λ at O: AO (hypothenuse) = 1 = C, AB = β = v/C = sin λ,BO = cos λ

If an electron has speed β = AB = 0.866 C, then, => λ = 60° , => ΒΟ = cos λ= 0.5, => AO/ BO = cosec λ = 2 =
mass doubles is. (m = M) : restmass+massincrease= 2

m + M = cosec λ = 2
\frac{\Delta t}{\sqrt{\Delta t^2-\Delta x^2}} = \frac{1}{\sqrt{1 - \left( \frac {\0.866 }{\1 } \right )^2}}

P.S. could you tell me what is space-contraction and time-dilation in this example (0.5-2)?

I'm following with interest your academical debate. I'd like to propose an interesting case that might help give insight to effects of SR:
consider a spaceship orbiting at r= C around the Earth at v = 0.866 C, communicating via radio in real time...
(...let's dispose of smokes and mirrors...).
If you are interested I'll give details. But probably you'll figure out the funny consequences by yourself.
(btw, you could detect space-contraction with your own eyes or measure it inside the ship in a simple manner, child's play.)