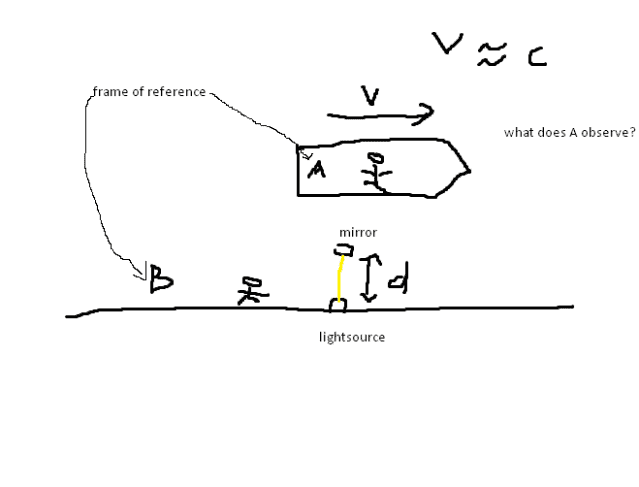
John232 said:
No problem, I have wrestled with this idea for some time. I still haven't been able to get an answer that resovles the confusion of this issue. I have thought about trying to publish my own theory of special relativity that only switchs the time variables and doesn't consider the time as being a change in time, and I don't know how far into the mathematics I would have to go into other theories that depend on this equation. I am sure it would find a lot of opposition since it would mean that everything we know about modern physics could be slightly wrong, but their is a growing opionion that relativity may still need some work done on it inoder to obtain grand unification and that may conclude that relativity as we know is not the final answer. Or, that a more accurate theory could get rid of dark matter or something of the like, I think it could be that something that physics has been looking for...
Let me see if I can resolve your confusion so you won't be tempted to publish your own theory of special relativity.
Part of the confusion comes from a misunderstanding of the nomenclature. In the usual presentation of the Lorentz Transform the equations are stated with t' and x' on the left side of the equation and t and x on the right side of the equations. You shouldn't think of the primed symbols as being associated exclusively with just a primed frame like S' and the unprimed symbols associated exclusively with an unprimed frame like S. Rather, you should think of the LT as providing a way to convert the coordinates of any frame into the coordinates of any other frame and back again if you want. I think it is better to refer to each frame with unprimed symbols to avoid this confusion.
So, for example, let's say that you have an event in frame A at
t=18 and
x=10 and you want to find the coordinates in frame B moving at
0.6c in the x direction with respect to B. (I'm going to use compatible units where c=1.) First we need to calculate gamma, γ and note this is not the English letter y, it is the Greek letter γ. You can get it by going to the advanced editing mode and clicking on the fourth Quick Symbol in the second row. Unfortunately, it looks very much like the letter y but you can tell the difference with the tail going straight down instead of angled.
OK, since β=0.6, we can calculate γ:
γ = 1/√(1-β
2) = 1/√(1-0.6
2) = 1/√(1-0.36) = 1/√(0.64) = 1/0.8 = 1.25
Now we are ready to apply the LT formulas:
t' = γ(t-xβ) = 1.25(18-10*0.6) = 1.25(18-6) = 1.25(12) =
15
x' = γ(x-tβ) = 1.25(10-18*0.6) = 1.25(10-10.8) = 1.25(-0.8) =
-1
So if we represent the coordinates as [t,x], then [18,10] in frame A is [15,-1] in frame B.
Now if we want to go back the other way, we do the same thing except that now frame A is moving at -0.6c along the x-axis with respect to frame B. Gamma is of course the same value.
t' = γ(t-xβ) = 1.25(15-(-1)*(-0.6)) = 1.25(15-0.6) = 1.25(14.4) =
18
x' = γ(x-tβ) = 1.25(-1-15*(-0.6)) = 1.25(-1+9) = 1.25(8) =
10
We have confirmed that [15,-1] in frame B transforms to [18,10] in frame A, the original coordinates that we started out with.
So you see, the primed symbols can apply temporarily to either frame, they are just intended to mean the new values in whatever frame you are converting the coordinates into. It's also important to recognize that the values that t and x refer to are coordinate values, that is, coordinate time and coordinate distance.
Now I want to get to the confusion over the Time Dilation factor. Since we use t' and t in the Lorentz Transform for two different frames, we don't want to use both of these symbols in the Time Dilation formula because they are both coordinate times (t' being used just temporarily). The Time Dilation formula applies in just a single frame and allows us to determine the time on a moving clock in that frame so we use Einstein's symbol for Proper Time, the Greek letter tau, τ. Einstein presented this formula as τ=t√(1-v
2/c
2) but it is more common to see it τ=t/γ. When presented these ways, there is no confusion because τ is always the Proper Time for the moving clock and t is always the Coordinate Time for the stationary clocks.
So if we want to find out how much time progresses on a clock moving at 0.6c in any frame compared to the coordinate clocks, it is simply 0.8 times the progress of time on the coordinate clocks (since 1/1.25=0.8).
Now let's consider a clock that starts at the origin in our Frame A from above and moves in a straight line at a constant speed to the event [18,10]. What speed will it move at? That's pretty easy to calculate because it has traveled a distance of 10 in a time of 18 so the speed is 0.555556c. If the time on the clock was 0 at the start of the trip, what time will be on the clock when it reaches 10? First we have to calculate gamma, like we did before:
γ = 1/√(1-β
2) = 1/√(1-0.555556
2) = 1/√(1-0.308642) = 1/√(0.691358) = 1/0.831479 = 1.202676
Then we divide the coordinate time of 18 by 1.20267 and we get
14.96663.
We could have used the Lorentz Transform calculate the coordinates in Frame C moving at 0.555556c to arrive at this same value as follows:
t' = γ(t-xβ) = 1.202676(18-10*0.555556) = 1.202676(18-5.55556) = 1.202676(12.44444) =
14.96663
x' = γ(x-tβ) = 1.202676(10-18*0.555556) = 1.202676(10-10) = 1.202676(0) =
0
Well, look at this, the distance coordinate came out zero and the reason why is because we have gone from Frame A in which the clock was moving at 0.555556c to Frame C in which it is stationary so the x-coordinate better come out zero because that is where it started and it isn't moving in Frame C.
Now the final point of confusion has to do with length contraction and why the distance coordinate isn't also divided by gamma in the Lorentz Transform. The answer to that question has to do with that zero coordinate for distance. In order to properly arrive at the correct time dilation factor, we had to use an event in Frame A that would result in a coordinate of zero (because the clock started at location zero in Frame A) for distance in Frame C. This happens automatically when we calculate where the clock is, based on its speed in Frame A.
But in order to see the correct length contraction, we have to use two events in Frame A that result in the time coordinates being the same at both ends of the desired length in Frame C. How do we do that? There are several ways but the easiest is to simply multiply the distance coordinate by the speed and use the same x-coordinate as before.
Remember, what we are trying to do is calculate the distance that the clock thinks it has traveled in Frame C. So starting from Frame A the clock moved from [0,0] to [18,10]. In Frame A, the distance is 10 and we expect it to be divided by gamma resulting in a value of
8.314794. All we have to do is multiply the distance coordinate by the speed so that is 10 times 0.555556 which is 5.55556 and we create a new event of [5.55556,10] in Frame A which we transform to Frame C:
t' = γ(t-xβ) = 1.202676(5.55556-10*0.555556) = 1.202676(5.55556-5.55556) = 1.202676(0) =
0
x' = γ(x-tβ) = 1.202676(10-5.55556*0.555556) = 1.202676(10-3.08642) = 1.202676(6.91358) =
8.314794
Here we see the requirement that the time coordinate is the same as it was when the clock started moving and this gives us the same length contraction for the distance the clock traveled as when we simply divide the original length by gamma.
Keep in mind that this is an easy calculation because one end was at the origin. If you are calculating the length of an object or a distance in which neither end is at the origin, you need to multiply the speed by the delta between the two ends and then add that number to the time coordinate of the first event.
I hope if you study this, all your confusions will be cleared up and you won't have to publish your own theory.