- #1
faen
- 140
- 0
So I was reading the proof of time dilation. It explains how the observer in a rest frame observes a longer path of the light than the observer in the moving frame.
However, I made a drawing of a slightly different experiment, where I can't predict the result of it. I was hoping somebody could help me out. In the picture below, the person in frame of reference A is moving close to the light speed. In the rest frame an observer is sending light between two vertical points as shown in the picture. The person in the rest frame would see that the light goes between the two points in time t determined by the given distance d and velocity c. Now, I am wondering what would the person in frame of reference A observe? If time is really slower for him, he would have to observe a shorter path with the same speed. However as far as I can see, the c and d variables is the same for the people in both frame of references giving equal time? I hope somebody can help me out with my confusion here, thanks a lot :)
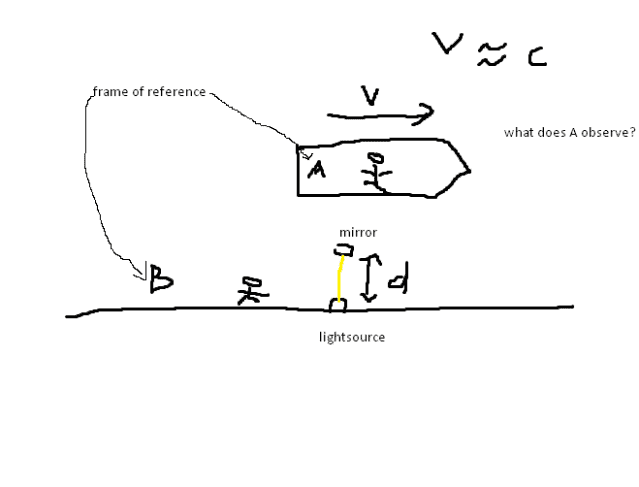
However, I made a drawing of a slightly different experiment, where I can't predict the result of it. I was hoping somebody could help me out. In the picture below, the person in frame of reference A is moving close to the light speed. In the rest frame an observer is sending light between two vertical points as shown in the picture. The person in the rest frame would see that the light goes between the two points in time t determined by the given distance d and velocity c. Now, I am wondering what would the person in frame of reference A observe? If time is really slower for him, he would have to observe a shorter path with the same speed. However as far as I can see, the c and d variables is the same for the people in both frame of references giving equal time? I hope somebody can help me out with my confusion here, thanks a lot :)