A SR experiment in which an entity exists in frame A but not frame B

[GregAshmore]

This paper by Cacioppo and Gangopadhyaya deals with two variations on the Pole and Barn paradox. Both paradoxes are successfully resolved. However, with regard to the first paradox, an electromagnetic wave comes into being in one frame, but not in the other. I consider this to be a paradox in its own right.

The scenario is a battery which slides on a rail. At one end of the battery is the positive terminal; the negative terminal is at the other end. There is a small gap between each terminal and the rail.

At a certain spot on the rail is a copper plate. The rest length of the plate is the same as the rest length of the battery. The thickness of the plate is the same as the gap between the terminals and the rail.

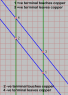
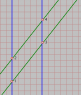
The battery moves along the rail at some fraction of light speed. An observer at rest on the rail will find that the battery is shorter than the plate, so that for some elapsed time both terminals are in contact with the plate. An observer at rest on the battery will find that the plate is shorter than the battery, so that there is never a time at which both terminals are in contact with the plate.

The paradox is presented this way: In the rail frame, the battery is shorted, but in the battery frame it is not.

The paradox is resolved by this note: "[In the rail frame a] circuit is not made until the negative terminal reaches the copper section, at which time the information that the negative terminal is now on the copper section must reach the forward (positive) terminal in order for the circuit to be completed." It is then shown that the information, which travels at the speed of light, cannot reach the positive terminal before it loses contact with the plate. Hence, the battery is not shorted.

While it is true to say that the battery is not shorted, that is not the whole story. The information that the second terminal has come into contact with the plate travels from terminal to terminal in the form of an electromagnetic wave. That wave comes into existence at the instant the rear terminal makes contact with the plate, and ceases to exist when the front terminal loses contact with the plate.

In the battery frame, there is never a time when both terminals are in contact with the plate.

The electromagnetic wave is a physical entity that exists in the rail frame, but not in the battery frame.

Have I got this right?

 

[pervect]

We had a roughly similar paradox in the past. My observation then was that lumped circuit theory didn't really work relativistically.

Specifically, Kirkhoff's current law takes a hit (though the relativistic continuity equations work just fine, it's no longer true that wires are neutral in all frames). More relevantly, Kirchoff's voltage law also takes a hit the intergal of the voltage around the loop depends on the observer.

I'm not sure where to go for further information - I do recall that my old E&M textbook derived lumped circuit theory from Maxwell's equations as an approximation valid under the correct circumstances, but I don't recall how they did it.

I advocated using non-lumped circut theory - if you have a nearby groundplane, you can then treat the copper strip in your example as a transmission line.

It may or may not be possible to "patch up" lumped circuit theory somehow (perhaps using retarded potentials) so that it makes sensible relativistic predictions. However, I'm not sure how to do this. The paper's treatment is a bit superficial.

Going back to the transmission line approach - what will happen when the positive terminal battery reaches the transmision ine is that some current will flow. If the internal inductance of the battery is low enough, the current flow would be equal to V/Z, V being the voltage of the battery and Z being the characteristic impedance of the transmision line it's charging.

The details of what happens are rather complex and I'd need to calcluate them, but basically the copper sheet woul wind up mostly being charged up first to the potential of th positive end of the battery +V, then discharged to the potential of the negative end of the battery. I'm not sure if the charging would be complete or not without more analysis, but some charging would occur.

So basically current would be flowing, but it would be mostly controlled by capacitance and /or inductance.

 

[Mentz114]

The electromagnetic wave is a physical entity that exists in the rail frame, but not in the battery frame.

In this case we could have a bomb paradox. If a detector is wired to a bomb in each frame, then they must both detect or not detect the wave.

The waves begin when the first electrode touches the copper - one backwards through the battery, and one forward through the copper. This happens in both frames.

 

[Dale]

That wave ... ceases to exist when the front terminal loses contact with the plate.

I don't think this is correct. Can you justify it?

 

[GregAshmore]

I've read all three replies. I'll respond in this one reply.

First, to DaleSpam: No, I cannot justify my statement that the wave ceases to exist when the front terminal loses contact with the plate. As I wrote the post, I figured that the wave would not degrade instantaneously. I started to say something about the wave degrading over time, but I don't know enough about the dynamics of an open circuit to say how that degradation would proceed. I decided to waffle a bit and use the potentially ambiguous word "when". I did this on the grounds that, in the context of this discussion, it doesn't matter too much how the wave degrades; the main thing is that it exists in one frame and not the other.

To pervect and Mentz144: As I thought about the problem, I wondered whether the leading terminal would begin to charge the plate as it made contact, even before the trailing terminal made contact. I decided to follow the lead of the paper, which does not begin to consider transfer of "information" until both terminals have made contact.

Presumably, the decision to ignore (or assume no) movement of charge until both terminals are in contact with the plate was a conscious simplification of the scenario. This simplification allowed the authors to make a point about the transmission speed of electrical signals, but at the cost of introducing another [seeming] paradox.

I found the paper while I was looking for a solution to a problem in Taylor and Wheeler. In T&W, there is an open circuit with a battery, lamp, and two rails. One rail is tied to the negative terminal of the battery. The other rail is tied to one end of the lamp filament (yes, it's shown as a wound filament). There is a gap in one rail. The slider is exactly as wide as the gap when both are at rest. So, when both are at rest, the lamp glows steadily. The question is whether the lamp will flicker as the slider whizzes by.

I (finally) understand length contraction and relativity of simultaneity enough to be sure that the slider will be out of contact with the rail for some period of time. Then it became a question of how the electrical circuit would behave. As I thought about the inductance in the filament, capacitance in the battery, etc, etc, all in a relativistic system, I got a headache. So I did what you can't do in class--I asked Mr. Google for help. I found the paper referenced above, which uses a simplified version of the apparatus in T&W. I also found the paper by G. P. Sastry on which the T&W problem is based. The two papers use the same method to resolve the paradox.

Now, it's obvious that there is no simple solution to the problem. Yet, a simple solution was offered. This reminds me of why I was so skeptical of what I read about relativity as I started: Most of the experiments in the books have never been run in a lab. It's easy to say things when you don't have to run the experiment to prove that you are right.

I'm mostly past that skepticism, having worked enough problems, and plotted the results on a spacetime diagram, to see that the theory is self-consistent, and to understand why the behavior of high speed particles (for example) does support the theory.

Still, it would be nice if people didn't pretend that everything is cut and dried.

 

[Dale]

the main thing is that it exists in one frame and not the other.
...
Still, it would be nice if people didn't pretend that everything is cut and dried.

I agree with your point about the oversimplification, but I am highly skeptical of the claim that a wave exists in one frame and not the other. I think that their analysis resolving the paradox was over simplified, but I think your analysis introducing a new paradox is also over simplified.

 

[PeterDonis]

The electromagnetic wave is a physical entity that exists in the rail frame, but not in the battery frame.

No, this is not correct. The EM wave exists in both frames, and in both frames, it fails to reach the positive terminal in time to complete a circuit.

Call the event when the negative terminal of the battery makes contact with the copper plate event N. Call the event when the positive terminal of the battery *loses* contact with the copper plate event P. By hypothesis, events N and P are spacelike separated.

At event N, an EM wave is created and propagates towards the positive terminal of the battery at the speed of light. However, since event P is spacelike separated from event N, the EM wave can't possibly reach the positive terminal of the battery before event P (where "before" here refers to the time ordering of events on the positive battery terminal's worldline, so the statement I just made is frame invariant). So the circuit can never be completed; but the EM wave emitted from event N exists in both frames.

 

[PeterDonis]

That wave comes into existence at the instant the rear terminal makes contact with the plate, and ceases to exist when the front terminal loses contact with the plate.

This is probably where the confusion lies. The wave does not cease to exist when the positive terminal loses contact with the plate; it ceases to exist when it reaches the positive terminal and discovers that the positive terminal has already lost contact with the plate. In other words, there some event on the positive terminal's worldline, call it event W, where the EM wave emitted at event N arrives; and this event is *after* event P (where again, this is a frame invariant statement because both events lie on the same timelike worldline). Event W is where the EM wave ceases to exist, and this is true in both frames.

 

[Nugatory]

I decided to waffle a bit and use the potentially ambiguous word "when"

In a paradox that involves relativity of simultaneity, the word "when" is not 'potentially' ambiguous - it is just plain ambiguous, and the paradox is created by exploiting that ambiguity. The paradox comes from the ambiguity, so when you decide to waffle a bit you aren't just taking a convenient verbal short-cut to describe a problem - you are creating the problem.
[EDIT]or at least making it possible to create the problem

 

[GregAshmore]

In a paradox that involves relativity of simultaneity, the word "when" is not 'potentially' ambiguous - it is just plain ambiguous, and the paradox is created by exploiting that ambiguity. The paradox comes from the ambiguity, so when you decide to waffle a bit you aren't just taking a convenient verbal short-cut to describe a problem - you are creating the problem.
[EDIT]or at least making it possible to create the problem

No, the paradox does not come from the ambiguity about the demise of the wave. The paradox arises at the creation of the wave, because the wave is created in one frame and not the other. The manner of its demise is not relevant to the paradox.

The authors treat the wave as coming into being at the instant that both terminals come into contact with the plate. This only happens in the rest frame of the plate. In the rest frame of the battery, there is never a time when both terminals are in contact with the plate; therefore, the wave never exists.

Granted, the paradox of the wave only comes about as the result of the simplification that the authors have made. If that simplification is unjustified, then the paradox of the wave goes away. Then, too, if that simplification is unjustified the authors have not resolved the paradox of the shorting battery.

 

[Nugatory]

The authors treat the wave as coming into being at the instant that both terminals come into contact with the plate.

"at the instant" sure sounds to me like an improperly specified "when"

 

[Dale]

The paradox arises at the creation of the wave, because the wave is created in one frame and not the other.

This is what I doubt. I think that any wave must be created in both frames.

 

[GregAshmore]

"at the instant" sure sounds to me like an improperly specified "when"

The discussion is of the incident as viewed from the rest frame of the plate. So the authors are talking about "when" in that frame.

 

[GregAshmore]

This is what I doubt. I think that any wave must be created in both frames.

The wave, as defined by the authors, comes into being at the instant in the rest frame of the plate at which both terminals come into contact with the plate. There is no instant in the rest frame of the battery at which both terminals are in contact with the plate, so the wave as defined by the authors cannot be created in that frame.

[Edit] It is perhaps important to note that the authors do not speak of an electromagnetic wave. They speak of information being transmitted from terminal to terminal at the speed of light. That transmission begins at the instant in the rest frame of the plate at which both terminals come into contact with the plate.

 

[Dale]

It is perhaps important to note that the authors do not speak of an electromagnetic wave.

I think that is important. You are the only one talking about a wave which exists in one frame and not in another. Whether or not there is a wave is irrelevant in one frame and important in the other frame, but that doesn't mean that the wave doesn't exist in both frames.

 

[GregAshmore]

Whether or not there is a wave is irrelevant in one frame and important in the other frame

Understood.

but that doesn't mean that the wave doesn't exist in both frames.

If the wave exists in a frame, it is due to some cause.
For each frame, let us inquire as to the cause of the wave.

What is the cause of the wave in the rest frame of the plate?
Here is the description in the paper:

the positive terminal contacts the copper section first, followed by the negative terminal. A circuit is not made until the negative terminal reaches the copper section, at which time the information that the negative terminal is now on the copper section must reach the forward (positive) terminal in order for the circuit to be completed.

The cause of the wave in the rest frame of the plate is the presence of both terminals on the plate. Presumably this is due to the establishment of a potential [edit] in the plate [end edit] from terminal to terminal.

What is the cause of the wave in the rest frame of the battery?
If the wave exists in the rest frame of the battery, it cannot be due to the same cause as in the rest frame of the plate, because in the rest frame of the battery there is never a time when both terminals are in contact with the plate.

As seen in the rest frame of the battery, the wave comes into being when the leading edge of the plate reaches the negative terminal. At that time, the trailing edge of the plate has already passed the positive terminal; only the negative terminal is in contact with the plate. What would cause an electromagnetic wave to arise at that time?

 

[Nugatory]

As seen in the rest frame of the battery, the wave comes into being when the leading edge of the plate reaches the negative terminal. At that time, the trailing edge of the plate has already passed the positive terminal; only the negative terminal is in contact with the plate. What would cause an electromagnetic wave to arise at that time?

That's what always happens when you touch a conductor to one terminal of a battery. As long as there is any potential gradient in a conductor, charge flows in whatever way levels out the gradient; that's why in a static situation all parts of a conductor are at the same potential.

Usually we assume that the leveling happens instantaneously (all parts of the copper plate reach the same potential at the same time - there are those evil and treacherous words again!) but in this problem the speeds involved are high enough and the times short enough that we have to allow for the propagation time.

 

[Dale]

As seen in the rest frame of the battery, the wave comes into being when the leading edge of the plate reaches the negative terminal.

As seen in both frames, that is when a wave would start. Why would it only be the rest frame of the battery?

The positive terminal has already charged the plate, regardless of whether it is still in contact or not. Capacitors retain their charge even when removed from the source.

 

[PeterDonis]

The wave, as defined by the authors, comes into being at the instant in the rest frame of the plate at which both terminals come into contact with the plate.

I don't think that's quite what they meant to say. Their description is vague, since they don't actually talk about what a "circuit" is, and as you note, they don't actually talk about an EM wave, but just about the "information" that the negative terminal is touching the copper propagating back to the positive terminal. But here's what I think they were trying to describe:

(1) When the positive terminal contacts the copper plate, an EM wave starts propagating from the positive terminal, through the plate, back towards the negative terminal. (As DaleSpam and Nugatory have noted, this EM wave charges the plate.)

(2) When the negative terminal contacts the plate, a "partial circuit" is formed, and an EM wave starts propagating back *through the battery* towards the positive terminal. (As DaleSpam noted, this EM wave is caused by the charge on the plate.)

(3) When the positive terminal loses contact with the copper plate, the wave that was propagating from it starts to die out; one could think of this as the end of an EM wave train propagating back through the plate towards the negative terminal.

(4) When the EM wave from the negative terminal reaches the positive terminal, it finds that it can't close the circuit because the positive terminal has lost contact with the plate.

(If the positive terminal were still in contact with the plate when the EM wave from the negative terminal reached it, the circuit would be closed, and what would close it would be the EM wave from negative to positive through the battery connecting up with the EM wave from positive to negative through the copper plate.)

 

[MikeLizzi]

I appear to have a different take on this problem. As far as I am concerned, the circuit never closes either from the reference frame of the battery or the plate. It's an issue of relativity of simultaneity.

Here is a web page with pictures and real calculated numbers

http://www.relativitysimulation.com/Documents/BatteryParadox2.htm

 

[PeterDonis]

the circuit never closes either from the reference frame of the battery or the plate.

I think everyone is in agreement on this. What's described on the page you linked to is basically what I described in posts #7 and #19, except that they are using a weird kind of clock synchronization. The issue appears to be more in the details of what would constitute the circuit closing, and what happens when a circuit is "partially closed" but not yet fully closed.

 

[Mentz114]

MikeLizzi, please point out my error, because these diagrams indicate ( to me ) that in the track frame, the -ve electrode touches the copper while the +ve electrode is in contact. The rest length of the battery is the same as the rest length of the copper. The relative velocity is 0.80c.

There seems little doubt that the resolution is by treating the copper as a capacitor and looking at the charge/discharge cycle in each frame. The transient current will produce an EM pulse in both frames - and I'll bet the pulses are related by an LT boost. The state of the system will return to its initial state when the battery has passed, and there's no reason to expect any paradox.

 

[MikeLizzi]

I think everyone is in agreement on this. What's described on the page you linked to is basically what I described in posts #7 and #19, except that they are using a weird kind of clock synchronization. The issue appears to be more in the details of what would constitute the circuit closing, and what happens when a circuit is "partially closed" but not yet fully closed.

Oh, good. Sometimes I have trouble following (understanding) other peoples posts.

With regards to the graphics I referenced and clock synchronization;

In the scene, a reference frame is defined with origin at the center of the scene (call it S) at time t=0. Its velocity with respect to us, the observers is zero.

The plate is at rest with respect to S and at position +x. So the plate has no length contraction and all clocks attached to it display the same value.

The battery is moving to the right at .866c with respect to S at some distance –x. The battery has length contraction and clocks attached to the battery at different locations display different values (proper time). The clocks on the battery are running at half the rate of the clocks on the plate.

With regards to the meaning of “closed circuit” I would offer the definition that the circuit is closed when the following condition applies:
1. The plate is in contact with terminal t1 when the proper time for the clock on t1 displays tc
2. The plate is in contact with terminal t2 when the proper time for the clock on t2 displays tc
And that never happens.

 

[MikeLizzi]

MikeLizzi, please point out my error, because these diagrams indicate ( to me ) that in the track frame, the -ve electrode touches the copper while the +ve electrode is in contact. The rest length of the battery is the same as the rest length of the copper. The relative velocity is 0.80c.

There seems little doubt that the resolution is by treating the copper as a capacitor and looking at the charge/discharge cycle in each frame. The transient current will produce an EM pulse in both frames - and I'll bet the pulses are related by an LT boost. The state of the system will return to its initial state when the battery has passed, and there's no reason to expect any paradox.

There is nothing wrong with your diagrams as far as I can see. They say that, in the reference frame of the battery, the time intervals when the terminals are touching the plate don’t overlap. In the reference frame of the plate, the time intervals do overlap. The issue is really the definition of a closed circuit. I offered a definition in my response to PeterDonis.

 

[PeterDonis]

With regards to the meaning of “closed circuit” I would offer the definition that the circuit is closed when the following condition applies:
1. The plate is in contact with terminal t1 when the proper time for the clock on t1 displays tc
2. The plate is in contact with terminal t2 when the proper time for the clock on t2 displays tc
And that never happens.

It's true that this never happens in the scenario as given, because the plate is shorter than the battery in the battery's rest frame. However, this is not the strictly correct meaning of "closed circuit", because it takes time for current to travel from one end of the battery or the plate to the other.

The strictly correct meaning of "closed circuit" is that the events I labeled N and P in previous posts--the event of the negative battery terminal making contact with the plate, and the event of the positive battery terminal losing contact with the plate--are timelike separated. (If they are null separated, we have an "edge case" where there is only a closed circuit for an instant.) In the scenario as it was given, neither of our conditions for a closed circuit are satisfied; but one could construct scenarios where your condition was satisfied but mine was not.

 

[MikeLizzi]

It's true that this never happens in the scenario as given, because the plate is shorter than the battery in the battery's rest frame. However, this is not the strictly correct meaning of "closed circuit", because it takes time for current to travel from one end of the battery or the plate to the other.

The strictly correct meaning of "closed circuit" is that the events I labeled N and P in previous posts--the event of the negative battery terminal making contact with the plate, and the event of the positive battery terminal losing contact with the plate--are timelike separated. (If they are null separated, we have an "edge case" where there is only a closed circuit for an instant.) In the scenario as it was given, neither of our conditions for a closed circuit are satisfied; but one could construct scenarios where your condition was satisfied but mine was not.

I think our conditions are identical. Yours is just phrased in more sophisticated language.
I can try any version of the OP's problem that anyone thinks will violate my conditions using my simulation program. This is, after all, just the "Pole-in-the-Barn" paradox with some diversionary electrical circuitry thrown in. I've run hundreds of versions of the "Pole-in-the-Barn" paradox during program testing.

 

[PeterDonis]

I think our conditions are identical.

No, they're not. Your condition says that event P must be later than event N in the battery's rest frame. It is perfectly possible for that to be the case but still have events N and P spacelike separated; just have the time interval between N and P, in the battery's rest frame, be less than the light-travel time between the terminals in the same frame (i.e., the distance in that frame divided by c). If this is the case, your condition is met but mine is not.

 

[MikeLizzi]

No, they're not. Your condition says that event P must be later than event N in the battery's rest frame. It is perfectly possible for that to be the case but still have events N and P spacelike separated; just have the time interval between N and P, in the battery's rest frame, be less than the light-travel time between the terminals in the same frame (i.e., the distance in that frame divided by c). If this is the case, your condition is met but mine is not.

Wow. Maybe I stated my conditions poorly because the requirement you stated isn't required.

Can you give me some numbers for starting conditions? Then I can see for myself.

 

[GregAshmore]

I think we would all agree that the solution presented in the paper is oversimplified, in that it deals with flow of charge only while both terminals are in contact with the plate.

That simplification is the root of my argument that there exists an em wave in one frame but not the other, for under the simplified conditions, charge flows in one frame but not the other. However, my objection is to an overly simplistic approach to a problem, not to SR itself.

To resolve the paradox of the shorting battery, I will consider the flow of charge at each of the four events in the sequence. (I do not try to define "closed circuit".)

In the following I summarize the events qualitatively. My conclusion is that in both frames some quantity of charge is transferred from the positive terminal to the negative terminal of the battery. Whether that quantity of transferred charge would be calculated to be the same in both frames I'm not prepared to say. I will note, however, that the total elapsed time during which charge flows is greater in the rest frame of the plate than in the rest frame of the battery.

Assume that at the start of the experiment the plate is at the same potential as the negative terminal of the battery.

The four events are these:
EvA: Positive terminal of battery meets leading edge of plate.
EvB: Positive terminal of battery meets trailing edge of plate.
EvC: Negative terminal of battery meets leading edge of plate.
EvD: Negative terminal of battery meets trailing edge of plate.

The events are plotted on a spacetime diagram, below. The diagram is scaled with c = 1.
In the statement of the problem, the rest lengths of the plate and battery are equal. For this discussion, the lengths are set to 2. Thus, it takes 2 units of time for light to travel the rest length of the plate or battery.

To keep the graph readable, the relative speed is set to 0.6.

In the rest frame of the plate:

EvA: Positive terminal of battery meets leading edge of plate.
Position = 0
Time = 0
Charge begins to flow from the positive terminal of battery into the plate.



EvC: Negative terminal of battery meets leading edge of plate.
Position = 0
Time = 2.667

In the 2.667 units of elapsed time since its inception at event EvA, the wave of charge has had more than enough time to travel the 2.0 units of plate length. There is therefore no place on the plate that has not been affected to some degree by the charge from the battery. This means that at every point on the plate the potential is now higher than the potential at the negative terminal of the battery.

Because the positive terminal is still in contact with the plate, charge continues to flow from the positive terminal of the battery into the plate.

Because every place on the plate is at a higher potential than the negative terminal of the battery, charge begins to flow from the plate into the negative terminal of the battery.



EvB: Positive terminal of battery meets trailing edge of plate.
Position = 2.000
Time = 3.333

Charge stops flowing from the positive terminal of the battery into the plate.
Total time that charge flowed into the plate = 3.333 units.

Charge continues to flow from the plate into the negative terminal of the battery.



EvD: Negative terminal of battery meets trailing edge of plate.
Position = 2.000
Time = 6.000

Charge stops flowing from the plate into the negative terminal of the battery.
Total time that charge flowed out of the plate = 3.333 units.



In the rest frame of the battery:
EvA: Positive terminal of battery meets leading edge of plate.
Position = 0
Time = 0

Charge begins to flow from the positive terminal of battery into the plate.



EvB: Positive terminal of battery meets trailing edge of plate.
Position = 0
Time = 2.667

Charge stops flowing from the positive terminal of the battery into the plate.
Total time that charge flowed into the plate = 2.667 units.


EvC: Negative terminal of battery meets leading edge of plate.
Position = -2.000
Time = 3.333

Because the charging of the plate began at its leading edge, the leading edge of the plate is now at a higher potential than the negative terminal of the battery. Therefore, charge begins to flow from the plate into the negative terminal of the battery.



EvD: Negative terminal of battery meets trailing edge of plate.
Position = -2.000
Time = 6.000

Charge stops flowing from the plate into the negative terminal of the battery.
Total time that charge flowed out of the plate = 2.6667 units.



This image shows the four events as the battery slides by the plate.
Pole leading = positive terminal of battery
Pole trailing = negative terminal of battery
Barn = plate

 

[PeterDonis]

Wow. Maybe I stated my conditions poorly because the requirement you stated isn't required.

Here's how you stated the condition originally:

With regards to the meaning of “closed circuit” I would offer the definition that the circuit is closed when the following condition applies:
1. The plate is in contact with terminal t1 when the proper time for the clock on t1 displays tc
2. The plate is in contact with terminal t2 when the proper time for the clock on t2 displays tc

In the battery's rest frame, coordinate time is equal to proper time for both terminals (because their clocks are synchronized in that frame). Terminal t1 is negative, and terminal t2 is positive (at least, I'm assuming that was your intended labeling--but actually the condition as you state it is symmetric between t1 and t2 so it doesn't really matter anyway). So #1 says that event N (negative terminal making contact with plate) has to happen before time tc, and #2 says that event P (positive terminal losing contact with plate) has to happen after time tc. Thus, event N must occur before event P in the battery's rest frame.

Can you give me some numbers for starting conditions? Then I can see for myself.

Here are two sets of numbers; the first gives results consistent with the scenario as stated in the OP--neither of our closed circuit conditions are satisfied--while the second satisfies your condition but not mine. All numbers are given in the battery rest frame.

Common Definitions

The spatial origin of the frame is equidistant between the positive and negative terminals of the battery. The time origin is at the instant when the spatial origin passes the geometric center of the copper plate (i.e., battery and plate are mutually "centered" on each other). The battery has rest length 2, so the negative terminal is at x = -1, and the positive terminal is at x = 1. The plate is moving in the negative x direction in the battery rest frame;. We use units where c = 1.

Scenario A

In this scenario, the plate has rest length 2, the same as the battery, and the relative velocity of the plate and the battery is 0.866, so the length contraction factor is 2, and the plate appears to be of length 1 in the battery rest frame. This leads to the following coordinates for events N and P:

Event N: (t, x) = (0.5, -1)

Event P: (t, x) = (-0.5, 1)

Note that event N happens after event P in this frame, and the events are spacelike separated, so neither of our "closed circuit" conditions is met.

Scenario B

In this scenario, the plate has rest length 4, and the relative velocity of the plate and the battery is 0.6, so the length contraction factor is 1.25, and the plate appears to be of length 3.2 in the battery rest frame. The event coordinates now are:

Event N: (t, x) = (-0.6, -1)

Event P: (t, x) = (0.6, 1)

Note that event N happens *before* event P in this frame, so your "closed circuit" condition is met. But the events are still spacelike separated: a light signal emitted from event N will reach the positive terminal at x = 1 *after* event P. So my closed circuit condition is *not* met; and the circuit will not actually close, because by the time the current within the battery that is initiated at event N reaches the positive terminal, that terminal is no longer in contact with the plate, so the circuit can't be completed.

 

[PeterDonis]

my objection is to an overly simplistic approach to a problem, not to SR itself.

I agree with this objection.

(I do not try to define "closed circuit".)

Actually, your analysis makes the good point that the term "closed circuit" is ambiguous; a better approach is to ask whether any net charge is transferred between the battery terminals.

My conclusion is that in both frames some quantity of charge is transferred from the positive terminal to the negative terminal of the battery.

On your assumptions (which seem to me to be reasonable), there would be some net charge transferred for any relative velocity of plate and battery (less than the speed of light).

Whether that quantity of transferred charge would be calculated to be the same in both frames I'm not prepared to say.

Since the transferred charge is in principle directly observable, it should be the same in both frames by the principle of relativity. I haven't worked out in detail how this comes out, but my guess is that it has to do with the voltage between the terminals being different in the different frames; in the battery frame, when the total time of charge flow is smaller, the voltage is higher, hence the current flow is higher, so the total charge transferred is the same.

 

[MikeLizzi]

Here's how you stated the condition originally:



In the battery's rest frame, coordinate time is equal to proper time for both terminals (because their clocks are synchronized in that frame). Terminal t1 is negative, and terminal t2 is positive (at least, I'm assuming that was your intended labeling--but actually the condition as you state it is symmetric between t1 and t2 so it doesn't really matter anyway). So #1 says that event N (negative terminal making contact with plate) has to happen before time tc, and #2 says that event P (positive terminal losing contact with plate) has to happen after time tc. Thus, event N must occur before event P in the battery's rest frame.

Here are two sets of numbers; the first gives results consistent with the scenario as stated in the OP--neither of our closed circuit conditions are satisfied--while the second satisfies your condition but not mine. All numbers are given in the battery rest frame.

Common Definitions

The spatial origin of the frame is equidistant between the positive and negative terminals of the battery. The time origin is at the instant when the spatial origin passes the geometric center of the copper plate (i.e., battery and plate are mutually "centered" on each other). The battery has rest length 2, so the negative terminal is at x = -1, and the positive terminal is at x = 1. The plate is moving in the negative x direction in the battery rest frame;. We use units where c = 1.

Scenario A

In this scenario, the plate has rest length 2, the same as the battery, and the relative velocity of the plate and the battery is 0.866, so the length contraction factor is 2, and the plate appears to be of length 1 in the battery rest frame. This leads to the following coordinates for events N and P:

Event N: (t, x) = (0.5, -1)

Event P: (t, x) = (-0.5, 1)

Note that event N happens after event P in this frame, and the events are spacelike separated, so neither of our "closed circuit" conditions is met.

Scenario B

In this scenario, the plate has rest length 4, and the relative velocity of the plate and the battery is 0.6, so the length contraction factor is 1.25, and the plate appears to be of length 3.2 in the battery rest frame. The event coordinates now are:

Event N: (t, x) = (-0.6, -1)

Event P: (t, x) = (0.6, 1)

Note that event N happens *before* event P in this frame, so your "closed circuit" condition is met. But the events are still spacelike separated: a light signal emitted from event N will reach the positive terminal at x = 1 *after* event P. So my closed circuit condition is *not* met; and the circuit will not actually close, because by the time the current within the battery that is initiated at event N reaches the positive terminal, that terminal is no longer in contact with the plate, so the circuit can't be completed.

Oh, now I think I get what you mean.
But, the conditions I set are sufficient to resolve the paradox. They focus on relativity of simultaneity. Your additional level of preciseness (and that of the author of the OP reference) turns the thread into a discussion of circuit theory. Is it really worth it?

 

[PeterDonis]

But, the conditions I set are sufficient to resolve the paradox.

Only for an oversimplified view of what the "paradox" is. On a more comprehensive view, I'm not sure either of our conditions are the right ones. See below.

Your additional level of preciseness (and that of the author of the OP reference) turns the thread into a discussion of circuit theory. Is it really worth it?

As GregAshmore's follow-up post shows, the real question is whether there is any net charge transferred, and if his analysis is correct, neither of our conditions tells whether that happens, and how much.

 

[Dale]

After some thought, I don't think that it makes sense to try to formulate a relativistic definition of what constitutes a closed circuit. A closed circuit is part of circuit theory, and circuit theory rests on three assumptions, two of which seem to be violated for a relativistic circuit. Specifically, that none of the elements have a net charge and more importantly that electrical effects happen instantaneously (so called small circuit assumption).

 

[PeterDonis]

After some thought, I don't think that it makes sense to try to formulate a relativistic definition of what constitutes a closed circuit.

I agree; GregAshmore's latest post shows that a better question to ask is whether any net charge is transferred between the battery terminals.

 

[pervect]

The authors were not terribly clear about what the "wave" was, which is why I don't care for the paper much.

My interpretation of what they probably meant is that the wave is a physical wave of charge which flows through the metal strip, which as I mentioned before acts approximately like a transmission line.If that's not what they meant, I'm at a bit of a loss as to what they were trying to say.

[add]
It may be the case that what they are referring to as a wave is the so-called retareded potential, http://en.wikipedia.org/wiki/Retarded_potential
[end add]

Without a ground return, the problem is tricky to analyze and rather suspectible to the details of the environment. But if you envision it occurring out in an empty vacuum with nothing nearby, and you idealize the battery, basically you expect that when the positive terminal of the battery touches the metal, there will be a physical wave of + charge transmitted to the plate from the battery, which will spread at the speed of light (assuming a vacuum dielectric) through the metal. The plate will act like a transmission line with no ground plane (or a ground plane at infinity).

The battery will acquire a net negative charge in the process, which will spread through the casing of the battery at the speed of light as well.

The capacitance of the battery to infinity multipled by its charge will be equal to the capacitance of the charged section of plate to infinity multiplied by its charge.

With a non-ideal battery, you'll need to model its internal structure as well. Which would add a lot of complexity to the problem - but you might need to, since the dimensions of the battery has a longer proper length than the wire.

Basically,whichever approach you use, you'll need to carry out your analysis using Maxwell's equations, and not circuit theory.

That's the other reason I don't like the paper - they don't make this (rather obvious) fact clear, they don't even mention Maxwell's equations.
[add]But, if they are using the retarded potential formalism and just not making it clear, their results will automatically satisfy Maxwell's equations
[end add]Actually, as I think about it, the transmission line approach is still an approximation to what Maxwell's equations will predict. The transmission line approach assumes, for instance, that no energy is radiated away. The actual metal strip will radiate, so it will be a combination of transmission line and antenna..

The overall behavior should be very similar, but I suspect it would require a computer analysis to really solve for exactly what happens via Maxwell's equations if you want to model it to a high level of detial to include antenna losses and what sort of electromagnetic signal gets radiated exactly.

Also, if you include realistic boundary conditions, it will be rather sensitive to the environment. Transmission lines with ground planes at infinity don't have any huge theoretical obstacles (they still obey Maxwsell's equations) but when you try to actually build them their behavior will change at the wave of a hand (literally). Having a ground plane helps stabilize the behavior relative to the enviornment a lot.

[add]
So, in conclusion, there should be a physical wave of charge traveling at "c", and also a mathematical "retarded potential" which might also be said to move at "c".

 

[GregAshmore]

But, the conditions I set are sufficient to resolve the paradox. They focus on relativity of simultaneity. Your additional level of preciseness (and that of the author of the OP reference) turns the thread into a discussion of circuit theory. Is it really worth it?

Yes, it certainly is, in my view. SR is presented as able to correctly represent and predict the dynamic behavior of electrical components at high relative velocities. Seeing it do so, even if only in calculations of hypothetical arrangements of components, would be pretty cool, for lack of a better term.

The details intrigue me. For example, it is not enough to calculate that the net charge transferred from terminal to terminal is the same in both frames. The progression of the electromagnetic field must be one and the same in both frames. By that I mean that there can be only one "actual" or "real" history for the em field. (Of course, the observed values of the field will be different from frame to frame at any chosen world point, according to the transformation equations. There must be one history, transformed into any number of frames.)

Taking this idea one step further, the history of any individual electron must be the same in both frames. We cannot have an electron in motion relative to its neighbors in one frame, and stationary relative to its neighbors in the other. The reason for this particular stipulation will be clear in a moment.

It is not clear to me that my qualitative analysis would satisfy the requirement of one reality. It, too, is likely to be overly simplistic. (I take pervect's most recent post as indicating the same: the situation is highly complex.)

If we consider the em field, it might be possible to construct a common history from the two "frame narratives" in my qualitative analysis. The history of the em would have a common beginning and end in the two frames. In the beginning, the charge is flowing out of the positive terminal; in the end charge is flowing into the negative terminal.

The history in the middle of the episode is a bit trickier. By middle, I mean the period in which: a) the charged plate is in contact with neither terminal in the battery frame; and b) a constant (?) current is flowing in the plate frame. The magnitude of the em field might be the same in both frames--in one frame due to static charge, and in the other frame due to constant current.

However, even if the magnitude of the field is the same in the two frames, can the particle history be the same, with current in one frame but not the other?

 

[Dale]

The progression of the electromagnetic field must be one and the same in both frames. By that I mean that there can be only one "actual" or "real" history for the em field. (Of course, the observed values of the field will be different from frame to frame at any chosen world point, according to the transformation equations. There must be one history, transformed into any number of frames.)

That is guaranteed by the fact that Maxwells equations are invariant under the Lorentz transform.

 

[Mentz114]

But, the conditions I set are sufficient to resolve the paradox. They focus on relativity of simultaneity. Your additional level of preciseness (and that of the author of the OP reference) turns the thread into a discussion of circuit theory. Is it really worth it?

If you're referring to the link you gave showing some times on the clocks - I have to say I'm not convinced by that argument. There's no doubt that in the track frame both electrodes are in contact for a time, and in the battery frame they are not. There's no simultaneity problem with that. The resolution comes about by considering the flows of charge, and the fact that the time for the circuit to close is greater in the track frame than the battery frame.

 

[pervect]

If you're referring to the link you gave showing some times on the clocks - I have to say I'm not convinced by that argument. There's no doubt that in the track frame both electrodes are in contact for a time, and in the battery frame they are not. There's no simultaneity problem with that. The resolution comes about by considering the flows of charge, and the fact that the time for the circuit to close is greater in the track frame than the battery frame.

The notion of "a circuit" to my mind, isn't Lorentz invariant because it depends on the notion of simultaneity.

Which is why I say that circuit theory isn't quite the same thing as Maxwell's equations.

The paper seems to have some other defintion of a "circuit" in mind, perhaps using retarded potentials. But it's difficult to see exactly what they had in mind, at least from my first reading it wasn't terribly clear.

In any case, I think it's clear that charge will flow. It might help to replace the battery with a pair of charged spheres, one with a net + charge and the other with a net - charge, and analyze the resulting problem. The battery will be sort of like that, except there will be some mechanism that transports charge at some rate to attempt to keep the charge on the spheres constant. Said mechanism will not be and cannot be perfect.

 

[Mentz114]

The notion of "a circuit" to my mind, isn't Lorentz invariant because it depends on the notion of simultaneity.

Which is why I say that circuit theory isn't quite the same thing as Maxwell's equations.

The paper seems to have some other defintion of a "circuit" in mind, perhaps using retarded potentials. But it's difficult to see exactly what they had in mind, at least from my first reading it wasn't terribly clear.

In any case, I think it's clear that charge will flow. It might help to replace the battery with a pair of charged spheres, one with a net + charge and the other with a net - charge, and analyze the resulting problem. The battery will be sort of like that, except there will be some mechanism that transports charge at some rate to attempt to keep the charge on the spheres constant. Said mechanism will not be and cannot be perfect.

Well, you don't seem to be disagreeing with anything in my post, so it seems a bit ungracious to disagree with your assertion circuit theory is not Lorentz invariant.

If the battery potential is 10v and it has 10 ohm internal resistance, when the terminals are short circuited we get a steady current of 1 amp on our am(p)meter. Every observer will agree on that reading. If we had instruments that could detect potentials in the battery rest frame, the readings on those instruments would be invariant. So in what way could we detect this LT failure ?

 

[pervect]

Well, you don't seem to be disagreeing with anything in my post, so it seems a bit ungracious to disagree with your assertion circuit theory is not Lorentz invariant.

If the battery potential is 10v and it has 10 ohm internal resistance, when the terminals are short circuited we get a steady current of 1 amp on our am(p)meter. Every observer will agree on that reading. If we had instruments that could detect potentials in the battery rest frame, the readings on those instruments would be invariant. So in what way could we detect this LT failure ?

Every observer will agree on the reading, but not all observers will agree on I = dQ/dt, t being coordinate time. This is I believe how 3-current is defined (in terms of coordinate time). Would you disagree?

3-Current through a wire isn't any sort of Lorentz invariant, it's just the component of a 4-vector. The 4-vector as a whole is of course Lorentz invariant. But circuit theory doesn't use the 4-vector approach, it uses the non-covariant 3-vector.

If you boost a current loop you get the situation in https://www.physicsforums.com/showthread.php?t=631446, in which the 3-current varies from I*gamma to I/gamma.

The easy situation to analyze is a transverse boost, where because of time dilation, the current drops by a factor of gamma.

The case of a parallel boost gets a bit trickier - rather than get off topic I suggest referring to the original "boosting a current loop" post. BUt the point is that no, not everyone agrees that the current is equal to I in this situation. At least by my reckoning.

Ohms law is another example of something used in circuit theory that is not Lorentz invariant. You can write it in tensor form, but the standard circuit theory version isn't written that way.

Kirchoff's voltage law has some issues, too, I believe. The definition of "voltage around the loop" depends on then notion of simultaneity used. I believe that these isssues are highly relevant to the "paradox" in question.

So there are a lot of elements of circuit theory that are not Lorentz invariant -though Maxwell's equations certinaly are.

Let me point out on the experimental level that it would be a rather unusual battery that had a 10 ohm internal impedance at all. frequences from 0-100 Ghz. (It might be possible to design one with careful enough construction techniques - it doesn't seem fundamentally impossible like designing a battery with no internal impedance).

If one is trying to actually understand the actual physics of a real battery in the situation, the DC impedance of the battery would be mostly irrelevant. The lowest frequency of interest would be 1 / (2 pi t), t being the time of contact. So if t is on the order of 1 ns (a rather long wire or battery of 1 foot), you'd be in the Ghz region already as the lowest frequency of interest.

Actual circuits usually have capacitors across the battery placed at strategic locations to keep the impedance low across a range of frequencies, they don't rely on a battery having a low impedance at "high" frequencies. Usually you use a lot of such "bypass" capacitors, you scatter them around the circuit board strategically, near the source of things you need to bypass.

What's really important at high frequencies is capacitance - and lead inductance.

This suggests some obvious (to my mind) simplifications of the original thought experiment to avoid batteries (just use a capacitor, that's what you'd use realistcally anyway) but perhaps this is drifting away from the point (though if you wanted to actually carry out an experiment, it would be essential).

I still believe that the simple resolution of the issue is to say that Maxwell's equations are Lorentz invariant, but lumped circuit theory has various and sundry issues. There might be a way to cast circuit theory in a provably Lorentz invariant form, but I'm not aware of anyone who has actually done this.

 

[Mentz114]

Pervect, thanks for the detailed breakdown of the issues, some of which you've aired in previous posts here and elsewhere. The point I'm trying to make is that it is not relevant that no-one has modeled all these phenomena in a relativistic way because relativity already contains the resolution.

What I mean is this - the physical events that take place can be thought of as a skein of time-like and null worldlines representing electrons and other involved matter, and em radiation. The configuration of these 4D curves is the physics. And it is fundamental to SR that no relativistic effect can alter this.

For instance in the simple case of the electron moving relative to an electric field. Some observers see a magnetic field why ? Because otherwise the worldline of the electron would look different in that frame if it were not there. So relativistic effects are there to preserve the integrity of the fundamental configuration.

So we know there can be no paradox in the battery-track scenario, and efforts to explain this are purely academic exercises - and not being able to explain it actually means nothing at all.

Although it can be fun and instructive.

 

[pervect]

Pervect, thanks for the detailed breakdown of the issues, some of which you've aired in previous posts here and elsewhere. The point I'm trying to make is that it is not relevant that no-one has modeled all these phenomena in a relativistic way because relativity already contains the resolution.

What I mean is this - the physical events that take place can be thought of as a skein of time-like and null worldlines representing electrons and other involved matter, and em radiation. The configuration of these 4D curves is the physics. And it is fundamental to SR that no relativistic effect can alter this.

For instance in the simple case of the electron moving relative to an electric field. Some observers see a magnetic field why ? Because otherwise the worldline of the electron would look different in that frame if it were not there. So relativistic effects are there to preserve the integrity of the fundamental configuration.

So we know there can be no paradox in the battery-track scenario, and efforts to explain this are purely academic exercises - and not being able to explain it actually means nothing at all.

Although it can be fun and instructive.

I agree there isn't any paradox. I'm hoping that pointing out the correct way to get results will be helpful to some people.

Unfortunately, the dedicated "paradox hunter" seems to be mostly beyond reach (perhaps someday one will surprise me though by listening and understanding.)

The "paradox hunter", by focusing on ever-more complex problems, manages to avoid confronting the underlying issues (mostly related to the relativity of simultaneity) that cause their problems in understanding the theory.

Basically the way to actually learn a theory is to study simple examples, not complex ones.

Complex examples are good for creating fear, uncertainty, and doubt, debating, and generally "blowing smoke", but aren't usually very good for learning.

 

[Mentz114]

I agree there isn't any paradox. I'm hoping that pointing out the correct way to get results will be helpful to some people.

Of course.

My post is a bit whimsical if not tautological and off-topic.

However, I don't rate simultaneity as a major cause of confusion. For example, in the classic barn-pole scenario, the paradox is said to arise from a simultaneity issue. But actually there is no frame in which pressing the button and the door closing can be simultaneous. The resolution is that the time between these events ( which happen in the barn frame) is hugely dilated in the pole frame. So the resolution is by looking at clock rates - not simultaneity. I'm occupied for the next 12 hours, so I won't be able to reply to a storm of protest, should one arise.

 

[ghwellsjr]

I haven't read every detail of this thread but I don't think any of you have considered the fact that there is an EM wave and currents flowing in the copper plate even before the plate reaches a battery terminal which makes the analysis even more complicated.

 

[GregAshmore]

That is guaranteed by the fact that Maxwells equations are invariant under the Lorentz transform.

Not if, at the event in question, the conditions stated for one frame are fundamentally different than the conditions stated for the other frame. In the present discussion, the paper referenced in the original post stated (in effect) that, at one and the same event: a) charge is transferred from terminal to plate in the rest frame of the plate; b) no charge is transferred from terminal to plate in the rest frame of the battery.

Unfortunately, the dedicated "paradox hunter" seems to be mostly beyond reach (perhaps someday one will surprise me though by listening and understanding.)

The "paradox hunter", by focusing on ever-more complex problems, manages to avoid confronting the underlying issues (mostly related to the relativity of simultaneity) that cause their problems in understanding the theory.

Basically the way to actually learn a theory is to study simple examples, not complex ones.

Complex examples are good for creating fear, uncertainty, and doubt, debating, and generally "blowing smoke", but aren't usually very good for learning.

The problem in this case is that the simple approach leads to a new paradox. I didn't bring up transmission lines or antennas or capacitors; you folks introduced complexity in order to solve the problem. (I don't fault you for doing so.) I was quite happy with the solution in the referenced paper for a couple of days. It was only as I tried to picture the solution on a spacetime diagram that I realized that the em wave in the one frame does not exist in the other.

I haven't read every detail of this thread but I don't think any of you have considered the fact that there is an EM wave and currents flowing in the copper plate even before the plate reaches a battery terminal which makes the analysis even more complicated.

I suppose so, due to the field surrounding the moving terminal (as seen from the rest frame of the plate).

I doubt that there is a simple solution to the question posed in the referenced paper, or to the question posed in the similar problem in Taylor and Wheeler. Indeed, the qualitative analysis which I presented a few posts back has the same problem as the solution offered by the authors of the referenced paper.

The problem is this:
In a simple solution, we assume that when (in a frame) a terminal is not in contact with the plate, no charge is transferred from that terminal to the plate. If we choose any event from the middle part of the sequence, we will find that neither terminal is touching the plate in the rest frame of the battery, and both terminals are touching the plate in the rest frame of the plate. Consequently, in any simple solution, we will find charge passing from terminal to plate in the one frame but not the other. We will thus have an em field in the neighborhood of the terminal that exists in one frame but not the other.

 

[PeterDonis]

If we choose any event from the middle part of the sequence, we will find that neither terminal is touching the plate in the rest frame of the battery, and both terminals are touching the plate in the rest frame of the plate.

No, this is *not* what we will find. What we will find is that the events "from the middle part of the sequence" in the battery rest frame, where neither terminal is touching the plate, are *different* from the events where the terminals *are* touching the plate, in either frame. You mentioned spacetime diagrams; drawing one will make it obvious that whether or not a given terminal is touching the plate at a given event is frame invariant.

 

[GregAshmore]

No, this is *not* what we will find. What we will find is that the events "from the middle part of the sequence" in the battery rest frame, where neither terminal is touching the plate, are *different* from the events where the terminals *are* touching the plate, in either frame. You mentioned spacetime diagrams; drawing one will make it obvious that whether or not a given terminal is touching the plate at a given event is frame invariant.

My statement makes no sense: "If we choose any event from the middle part of the sequence, we will find that neither terminal is touching the plate in the rest frame of the battery, and both terminals are touching the plate in the rest frame of the plate."

It makes no sense because two spatially separated terminals cannot be at one event.

The mental image that I had when I made the statement was based on the qualitative explanation several posts back. The times and positions in that explanation are from the spacetime diagram shown in that post. Even so, as I started to say what I meant in more precise terms, I found that the mental image I had formed of the process is not in agreement with the spacetime diagram. I'll need some time to think this through more carefully.

 

[pervect]

The problem in this case is that the simple approach leads to a new paradox. I didn't bring up transmission lines or antennas or capacitors; you folks introduced complexity in order to solve the problem. (I don't fault you for doing so.) I was quite happy with the solution in the referenced paper for a couple of days. It was only as I tried to picture the solution on a spacetime diagram that I realized that the em wave in the one frame does not exist in the other.

Which "em" wave are you referring to?

The "wave" of moving charges exists in all frames. There's also the "retarded potential".

I would guess that you're talking about the "em wave" in the paper, and my best guess is that they're talking about the retarded potential, so I'll answer it assuming that's what you meant, and assuming that's what the paper meant. (If you're complaining about the paper, I have to agree it's not terribly clear what it meant).

If you meant something else, we can have another go-around.

The retarded potential is a bit like a voltage. It's not really directly measurable (at least not classically). It's not uniquely defined because of the gauge condition, so you might regard it as a mathematical abstraction.

If you regard tensors as "existing" then it exists. If you require that it be able to be measured with some instrument, then it's just a mathematical abstraction (in all frames) because no instrument can measure the gauge part of it, the gauge part can be set arbitrarily (within certain rules.

There's no interpretation of the retarded potential that meets your criterion of "existing in one frame and not another" that I can see. you can regarded as "existing" or "being a mathematical abstraction" sensibly, depending on the details of what you mean by "exist", but the question of its "existence" doesn't depend on the frame in any way.

I doubt that there is a simple solution to the question posed in the referenced paper, or to the question posed in the similar problem in Taylor and Wheeler. Indeed, the qualitative analysis which I presented a few posts back has the same problem as the solution offered by the authors of the referenced paper.

The problem is this:
In a simple solution, we assume that when (in a frame) a terminal is not in contact with the plate, no charge is transferred from that terminal to the plate. If we choose any event from the middle part of the sequence, we will find that neither terminal is touching the plate in the rest frame of the battery, and both terminals are touching the plate in the rest frame of the plate. Consequently, in any simple solution, we will find charge passing from terminal to plate in the one frame but not the other. We will thus have an em field in the neighborhood of the terminal that exists in one frame but not the other.

The way I see it is this. This is a variant of the barn and the pole paradox. In the barn and the pole paradox, we learn that rigid bodies are idealizations that don't exist.

In this refinement of the barn-and-pole paradox, we learn that lumped circuit elements don't exist. They are rather similar to rigid bodies, in that they are overly simple.

A rigid body is defined by a small set of numbers - it's position, and rotation. The equations that model it are simple differential equations.

A nonrigid body is defined by a "fluid". The equations that model it are partial differential equations.

The lumped circuit elements are also defined by a small set of numbers - charge for a lumped capacitor, current for a lumped inductor.

Their equations of lumped circuit elements, in ordinary circuit theory, are described by ordinary differntial equations.

This is only an approximation. Real, physical circuit elements need to be described by fields. The equations that describe these fields are partial differential equations, Maxwell's equations.

Lumped circuit elements, are, like rigid bodies, only approximations. The actual description of a bodies state requires more than a few numbers.

If you start to draw off charge from a capacitor, let's say you put a discharging wire on the left side of the plate, the voltage on the right side of the plate does not jump instantaneously, faster than light. The charge has to flow across the plate, through the wire.

You can try to make a "paradox" out of this. Nothing can move faster than light but in your lumped circuit model, the right side of the plate discharges instantaneously when you connect the wire to the left side of the plate.

But there isn't any "paradox". There is only a model that's insufficiently advanced - a model that's trying to describe what needs to be describe by fields and partial differential equatons by "avereages" of the fields and ordinary differential equations.