Calculating Mary's Moped Speed: Solving for Maximum Velocity

[plane]

hey guys i am stumped on this question:

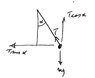
mary dangles her watch from a thin piece of string, while burning rubber on her supercharged moped. she notices that the string makes an angle of 15degrees with respect to the vertical while the moped accelerates to maximum speed, which takes about 18s. what is the maximum speed of mary's moped?

i am really stuck on this question and i need to show my work too. can anyone please help? thanks.

 

[Tide]

What, exactly, have you done so far?

 

[Fermat]

All you have to do is work out the acceleration on the watch/moped.
The watch is at an angle of 15 deg.
Draw a diagram of the forces on the watch. What are the only forces acting ?
From this, you should be able to get the acceleration.

 

[plane]

i can't get anything, i just keep staring at the diagram but i can't figure it out, how do i figure out the acceleration by using the angle? do i brake it into the X and Y components? then what?

 

[plane]

is there no one that can help me?

 

[plane]

All you have to do is work out the acceleration on the watch/moped.
The watch is at an angle of 15 deg.
Draw a diagram of the forces on the watch. What are the only forces acting ?
From this, you should be able to get the acceleration.

the only forces acting are the force of gravity (mg) and Ft (tension)

 

[Fermat]

Have you got the diagram ?

What forces have you got labelled on it ?

 

[Fermat]

Ah, already answered.

So, now resolve the Tension, Ft, into horizontal and vertical components.

 

[plane]

Ah, already answered.

So, now resolve the Tension, Ft, into horizontal and vertical components.

how? it only gives me the angle and the time, no forces or mass of the watch.

 

[Fermat]

If you know the angle the tension is acting at, can't you just then resolve the tension, call it Ft, into horizontal and vertical components using that angle ?


Take the mass of the watch as m.

 

[plane]

If you know the angle the tension is acting at, can't you just then resolve the tension, call it Ft, into horizontal and vertical components using that angle ?

Where did the time come from ?

Take the mass of the watch as m.

so this is what id be doing:

Ftcos15= Ftx
Ftsin15= Fty

and then Ftx= m(ax)?

then what do i substitute?

the time comes from:
accelerates to maximum speed, which takes about 18s. what is the maximum speed of mary's moped?

the question gives it to me

 

[Fermat]

Almost there.

Ft.cos15 is actually the vertical component.

You can equate this to the only other vertical force, the mass of the watch, hence you can get an expression for Ft.

 

[plane]

Almost there.

Ft.cos15 is actually the vertical component.

You can equate this to the only other vertical force, the mass of the watch, hence you can get an expression for Ft.

i always thought sine was the vertical componenet, when resolving vectors and i think that's true. also it doesn't give me the mass so how can i get an expression for Ft? can you please show me how?

 

[Fermat]

I'll upload a sketch.

The masss, m, should cancel out.,

 

[Fermat]

See attachment.

 

[Fermat]

What is your expression for Ft ?

 

[plane]

What is your expression for Ft ?

your attachment is pending approval, as for Ft i have no idea how to get an expression for it.

 

[Fermat]

You had two eqns,

Ftcos15= Ftx
Ftsin15= Fty

but they should have been,

Ftsin15= Ftx
Ftcos15= Fty

(You will see why the cos and sin are the other way around when the attachment is approved. But it's just really because the angle, alpha, is the angle to the vertical. If it had been the aqngle to the horizontal, then sin would have been the vertical component.)

The only vertical force is the mass of the watch, so Fty = mg. This gives,

Ftcos15= Fty = mg
==============

Now you have an expression for Ft, can you solve Ftx= m(ax) for a ?

 

[plane]

You had two eqns,

Ftcos15= Ftx
Ftsin15= Fty

but they should have been,

Ftsin15= Ftx
Ftcos15= Fty

(You will see why the cos and sin are the other way around when the attachment is approved. But it's just really because the angle, alpha, is the angle to the vertical. If it had been the aqngle to the horizontal, then sin would have been the vertical component.)

The only vertical force is the mass of the watch, so Fty = mg. This gives,

Ftcos15= Fty = mg
==============

Now you have an expression for Ft, can you solve Ftx= m(ax) for a ?

you have written an expression for FTy, but i need Ftx, is Ftx the same formula that being:
Ftsin15=Ftx=m(ax)?

 

[Fermat]

F_tsin15 = F_{t_x} = m(a_x)
F_tcos15= F_{t_y} = mg

F_tsin15 = m(a_x)
F_tcos15 = mg

Divide 1st eqn by 2nd eqn,

\frac{sin15}{cos15} = \frac{a_x}{g}

a_x = gtan15

 

[plane]

F_tsin15 = F_{t_x} = m(a_x)
F_tcos15= F_{t_y} = mg

F_tsin15 = m(a_x)
F_tcos15 = mg

Divide 1st eqn by 2nd eqn,

\frac{sin15}{cos15} = \frac{a_x}{g}

a_x = gtan15

thanks i get it now